题目内容
函数f(x)的定义域为D,若满足:①f(x)在D内是单调函数;②存在[a,b]⊆D,(a<b)使得f(x)在[a,b]上的值域也是[a,b],则称y=f(x)为闭函数. 若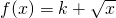 是闭函数,则实数k的取值范围是
是闭函数,则实数k的取值范围是
- A.

- B.
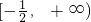
- C.

- D.

D
分析:先判定函数的单调性,然后根据条件建立方程组,转化成使方程x2-x-k=0有两个相异的非负实根,最后建立关于k的不等式,解之即可.
解答: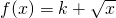 是单调增函数
是单调增函数
∴ 即使方程x2-x-k=0有两个相异的非负实根
即使方程x2-x-k=0有两个相异的非负实根
令f(x)=x2-x-k
∴ 解得k∈
解得k∈
故选D
点评:本题主要考查了函数的定义域及其求法,以及函数的值域,是高考的热点,属于基础题.
分析:先判定函数的单调性,然后根据条件建立方程组,转化成使方程x2-x-k=0有两个相异的非负实根,最后建立关于k的不等式,解之即可.
解答:
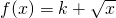 是单调增函数
是单调增函数∴
 即使方程x2-x-k=0有两个相异的非负实根
即使方程x2-x-k=0有两个相异的非负实根令f(x)=x2-x-k
∴
 解得k∈
解得k∈
故选D
点评:本题主要考查了函数的定义域及其求法,以及函数的值域,是高考的热点,属于基础题.

练习册系列答案
相关题目
若函数f(x)的定义域为[-1,2],则函数
的定义域为( )
| f(x+2) |
| x |
| A、[-1,0)∪(0,2] |
| B、[-3,0) |
| C、[1,4] |
| D、(0,2] |