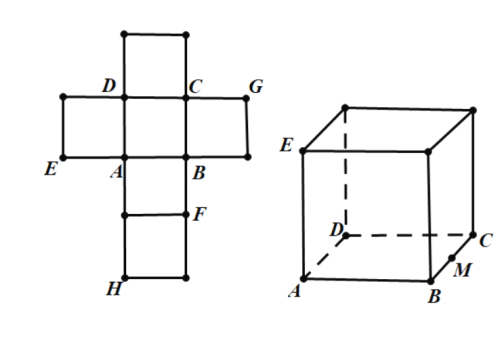
题目内容
【题目】若异面直线
所成的角是
，则以下三个命题:
①存在直线
，满足与的夹角都是；
②存在平面
，满足
，
与所成角为；
③存在平面
，满足
，与
所成锐二面角为.
其中正确命题的个数为（ ）
A. 0 B. 1 C. 2 D. 3
【答案】D
【解析】分析：在①中，在
上任取一点
，过作
， 
与
的夹角均为
；在②中，在
上取一点
,过作
；在③中，在上取一点
，过作，
确定一个平面平面
即可.
详解：异面直线
所成的角是，在①中，由异面直线所成的角是，
在上任取一点，过作，在空间中过点能作出直线，使得与的夹角均为，
存在直线，满足与的夹角都是，故①正确；
在②中，在上取一点,过作，则以确定的平面，满足
与
所成的角是，故②正确；在③中，在上取一点，过作，确定一个平面平面，过能作出一个平面
，满足
与所成锐二面角为，故③正确，故选D
练习册系列答案
相关题目
