题目内容
17．已知f（x）=x2-ax+$\frac{a}{2}$，在区间[0，1]上的最大值为g（a），求g（a）的最小值．分析 先求出函数的对称轴，通过讨论a的范围，从而求出g（a）的最小值．
解答 解：对称轴x=$\frac{a}{2}$，
①当$\frac{a}{2}$≤$\frac{1}{2}$时，此时函数最大值g（a）=f（1），
∴g（a）=1-a+$\frac{a}{2}$═1-$\frac{a}{2}$，其中a≤1，
∴当a=1时，g（a）有最小值$\frac{1}{2}$，
②当$\frac{a}{2}$≥$\frac{1}{2}$时，g（a）=f（0）=$\frac{a}{2}$，其中a≥1，
∴当a=1时，g（a）有最小值$\frac{1}{2}$，
综上所述，g（a）最小值为$\frac{1}{2}$．
点评 本题考查了二次函数的性质，考查分类讨论思想，是一道基础题．
练习册系列答案
相关题目
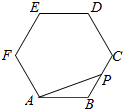如图所示：点P在正六边形ABCDEF上按A→B→C→D→E→F→A的路径运动，其中AB=4，则$\overrightarrow{AP}$•$\overrightarrow{AB}$的取值区间[-8，24]．
2．
在等腰梯形ABCD中，∠A=$\frac{π}{3}$，边AB、DC的长分别为2、1，若M、N分别是边BC、CD上的点，且满足|$\frac{\overrightarrow{BM}}{\overrightarrow{BC}}$|=|$\frac{\overrightarrow{CN}}{\overrightarrow{CD}}$|，则$\overrightarrow{AM}$•$\overrightarrow{AN}$的取值范围是（ ）
在等腰梯形ABCD中，∠A=$\frac{π}{3}$，边AB、DC的长分别为2、1，若M、N分别是边BC、CD上的点，且满足|$\frac{\overrightarrow{BM}}{\overrightarrow{BC}}$|=|$\frac{\overrightarrow{CN}}{\overrightarrow{CD}}$|，则$\overrightarrow{AM}$•$\overrightarrow{AN}$的取值范围是（ ）| A． | [$\frac{3}{2}$，+∞） | B． | （0，2] | C． | [$\frac{3}{2}$，3] | D． | （$\frac{3}{2}$，2） |