题目内容
已知曲线E:ax2+by2=1(a>0,b>0),经过点M(
,0)的直线l与曲线E交与点A、B,且
=-2
.
(1)若点B的坐标为(0,2),求曲线E的方程.
(2)若a=b=1,求直线AB的方程.
| ||
| 3 |
| MB |
| MA |
(1)若点B的坐标为(0,2),求曲线E的方程.
(2)若a=b=1,求直线AB的方程.
分析:(1)设A(x0,y0),进而可表示出
和
,再根据
=-2
,进而可求得x0和y0,点A的坐标可得,把点A,B的坐标代入曲线方程可求得a和b,进而可得曲线E的方程.
(2)设AB的中点位T,由条件得|TM|=|TA|-|MA|=
|AB|,|OM|=
,进而根据勾股定理联立方程求得|AB|和|OT|,进而可求得
tan∠OMT即直线AB的斜率,最后根据点斜式求得直线AB的方程.
| MB |
| MA |
| MB |
| MA |
(2)设AB的中点位T,由条件得|TM|=|TA|-|MA|=
| 1 |
| 6 |
| ||
| 3 |
tan∠OMT即直线AB的斜率,最后根据点斜式求得直线AB的方程.
解答:解:(1)设A(x0,y0),因为B(0,2),M(
,0)
故
=(-
,2),
=(x0-
,y0).
∵
=-2
.
∴(-
,2)=-2(x0-
,y0)
∴x0=
,y0=-1,即A(
,-1)
∵A,B都在曲线E上,所以
解得a=1,b=
∴曲线E的方程为x2+
=1
(2)设AB的中点为T,由条件得|TM|=|TA|-|MA|=
|AB|,|OM|=
根据Rt△OTA和Rt△OTM得,
即
,解得|AB|=
,|OT|=
∴在Rt△OTM中,tan∠OMT=
,
∴直线AB的斜率为
或-
∴直线AB的方程为y=
x-1或y=-
x+1
| ||
| 3 |
故
| MB |
| ||
| 3 |
| MA |
| ||
| 3 |
∵
| MB |
| MA |
∴(-
| ||
| 3 |
| ||
| 3 |
∴x0=
| ||
| 2 |
| ||
| 2 |
∵A,B都在曲线E上,所以
|
解得a=1,b=
| 1 |
| 4 |
∴曲线E的方程为x2+
| y2 |
| 4 |
(2)设AB的中点为T,由条件得|TM|=|TA|-|MA|=
| 1 |
| 6 |
| ||
| 3 |
根据Rt△OTA和Rt△OTM得,
|
即
|
| 3 |
| 1 |
| 2 |
∴在Rt△OTM中,tan∠OMT=
| 3 |
∴直线AB的斜率为
| 3 |
| 3 |
∴直线AB的方程为y=
| 3 |
| 3 |
点评:本题主要考查了椭圆的标准方程和直线与椭圆的关系.考查了学生综合分析问题和基本的运算能力.

练习册系列答案
相关题目
 的直线l与曲线E交与点A、B,且
的直线l与曲线E交与点A、B,且 .
. 的直线l与曲线E交与点A、B,且
的直线l与曲线E交与点A、B,且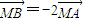 .
.