Question

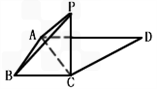
如图，已知四边形ABCD为直角梯形，∠ABC=90°，AD∥BC，AD=2，AB=BC=1，沿AC将△ABC折起，使点B到点P的位置，且平面PAC⊥平面ACD．
（I）证明：DC⊥平面APC；
（II）求二面角B﹣AP﹣D的余弦值．

Answer 1

（I）证明：∵∠ABC=90°，AB=BC=1，∴AC=
∵四边形ABCD为直角梯形，AD=2，AB=BC=1
∴CD=，
∴AC²+CD²=AD²，∴∠ACD=90°
∴DC⊥AC
∴平面PAC⊥平面ACD，平面PAC∩平面ACD=AC．
∴DC⊥平面APC；
（II）建立如图所示的空间直角坐标系，
则A（0，0，0），B（1，0，0），D（0，2，0），P（）
∴，=，
设平面APB的法向量为，
平面APD的法向量为
∴，
∴
∴可取
同理
∴=
∵二面角B﹣AP﹣D的平面角为钝二面角
∴二面角B﹣AP﹣D的余弦值为．