Question

求与直线l:5x-12y+6=0平行且到l的距离为2的直线的方程.

Answer 1

解法一：设所求直线的方程为5x-12y+C=0,

在直线5x-12y+6=0上取一点P₀(0,),

点P₀到直线5x-12y+C=0的距离为d=,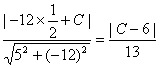

由题意得=2.

所以C=32或C=-20.

所以所求直线的方程为5x-12y+32=0和5x-12y-20=0.

解法二：设所求直线的方程为5x-12y+C=0,

由两平行直线间的距离公式得2=,解之得C=32或C=-20.

故所求直线的方程为5x-12y+32=0和5x-12y-20=0.