题目内容
在△ABC中,BC=1,AB=2,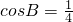 ,则sin(2A+B)的值为________.
,则sin(2A+B)的值为________.

分析:由余弦定理可得AC=2,B=C,∠A=180-2∠B.由
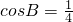 可得sinB的值,再由sin(2A+B)=sin(360°-3B)
可得sinB的值,再由sin(2A+B)=sin(360°-3B)=sin3B,利用三倍角公式,运算求得结果.
解答:由余弦定理可得 AC2=AB2+BC2-2AB•BC•cosB=4+1-2×2×1×
 =4,∴AC=2,
=4,∴AC=2,故△ABC为等腰三角形,B=C,∠A=180-2∠B.
由
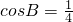 可得sinB=
可得sinB= ,故sin(2A+B)=sin(360°-3B)=sin3B=3sinB-4sin3B=
,故sin(2A+B)=sin(360°-3B)=sin3B=3sinB-4sin3B=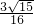 ,
,故答案为
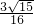 .
.点评:本题主要考查两角和差的正弦、诱导公式、余弦定理的应用,同角三角函数的基本关系,属于中档题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
在△ABC中,|BC|=2|AB|,∠ABC=120°,则以A,B为焦点且过点C的双曲线的离心率为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在△ABC中,(
+
)•
=|
|2,
•
=3,|
|=2,则△ABC的面积是( )
| BC |
| BA |
| AC |
| AC |
| BA |
| BC |
| BC |
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |