题目内容
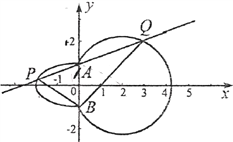
【题目】如图,点 ,点
,点![]() 是单位圆与
是单位圆与![]() 轴的正半轴的交点.
轴的正半轴的交点.

(1)若![]() ,求
,求![]() .
.
(2)已知![]() ,
,![]() ,若
,若![]() 是等边三角形,求
是等边三角形,求![]() 的面积.
的面积.
(3)设点![]() 为单位圆上的动点,点
为单位圆上的动点,点![]() 满足
满足![]() ,
,![]() ,
,![]() ,求
,求![]() 的取值范围.当
的取值范围.当![]() 时,求四边形
时,求四边形![]() 的面积.
的面积.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;
;![]()
【解析】
(1)根据任意角三角函数的定义先求出![]() ,即可求解.
,即可求解.
(2)由条件可得![]() ,再根据
,再根据![]() 是等边三角形,即可求出该等边三角形的高,从而可求解其面积.
是等边三角形,即可求出该等边三角形的高,从而可求解其面积.
(3)根据任意角三角函数的定义,可得![]() ,从而得
,从而得![]() ,
,
![]() ,即可求解
,即可求解![]() 的取值范围;根据
的取值范围;根据![]() ,再结合
,再结合![]() ,可得四边形
,可得四边形![]() 为菱形,从而可求解其面积.
为菱形,从而可求解其面积.
解:(1)由三角函数定义,可知![]() ,
,![]() ,
,
所以![]() .
.
(2)因为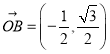 ,
,![]() ,
,![]() ,
,
所以![]() ,
,
所以![]() ,
,
又因为![]() 是等边三角形,
是等边三角形,
所以等边![]() 的高为1,边长为
的高为1,边长为![]() ,
,
因此![]() 的面积为
的面积为![]() .
.
(3)由三角函数定义,知![]() ,所以
,所以![]() ,
,
所以![]() ,
,
因为![]() ,所以
,所以![]() ,即
,即![]() ,
,
于是![]() ,所以
,所以![]() 的取值范围是
的取值范围是![]() .
.
当![]() 时,
时,![]() ,
,
即![]() ,解得
,解得![]() ,
,
易知四边形![]() 为菱形,此时菱形
为菱形,此时菱形![]() 的面积为
的面积为![]() .
.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
【题目】已知椭圆![]() 的中心在原点,焦点在
的中心在原点,焦点在![]() 轴上,离心率等于
轴上,离心率等于![]() ,它的一个顶点恰好在抛物线
,它的一个顶点恰好在抛物线![]() 的准线上.
的准线上.

![]() 求椭圆
求椭圆![]() 的标准方程;
的标准方程;
![]() 点
点![]() ,
,![]() 在椭圆上,
在椭圆上,![]() 是椭圆上位于直线
是椭圆上位于直线![]() 两侧的动点
两侧的动点![]() 当
当![]() 运动时,满足
运动时,满足![]() ,试问直线
,试问直线![]() 的斜率是否为定值,请说明理由.
的斜率是否为定值,请说明理由.
【题目】某港口的水深![]() (米)是时间
(米)是时间![]() (
(![]() ,单位:小时)的函数,下面是每天时间与水深的关系表:
,单位:小时)的函数,下面是每天时间与水深的关系表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
经过长期观测,![]() 可近似的看成是函数
可近似的看成是函数![]()
(1)根据以上数据,求出![]() 的解析式;
的解析式;
(2)若船舶航行时,水深至少要![]() 米才是安全的,那么船舶在一天中的哪几段时间可以安全的进出该港?
米才是安全的,那么船舶在一天中的哪几段时间可以安全的进出该港?