题目内容
已知向量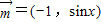 ,
,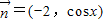 ,函数
,函数 .
.(1)求函数f(x)在区间
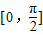 上的最大值;
上的最大值;(2)若△ABC的角A、B所对的边分别为a、b,
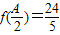 ,
,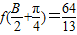 ,a+b=11,求a的值.
,a+b=11,求a的值.
【答案】分析:(1)利用两个向量的数量积公式求得f(x)=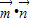 =4+sin2x,由
=4+sin2x,由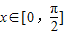 ,根据正弦函数的定义域和值域求得sin2x的范围,即可求得函数f(x)的值域.
,根据正弦函数的定义域和值域求得sin2x的范围,即可求得函数f(x)的值域.
(2)由 求得sinA的值;由
求得sinA的值;由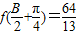 ,求得
,求得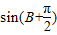 的值,从而求得cosB和sinB的值,再由正弦定理得
的值,从而求得cosB和sinB的值,再由正弦定理得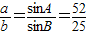 ,求得a的值.
,求得a的值.
解答:解:(1)依题意,f(x)=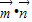 =2(2+sinxcosx)=4+sin2x…(3分),
=2(2+sinxcosx)=4+sin2x…(3分),
由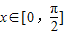 ,可得2x∈[0,π],sin2x∈[0,1],…(4分),
,可得2x∈[0,π],sin2x∈[0,1],…(4分),
所以,函数f(x)在区间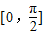 上的最大值为5.…(5分)
上的最大值为5.…(5分)
(2)由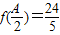 得
得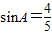 .…(6分),
.…(6分),
由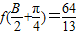 ,得
,得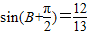 …(7分),从而
…(7分),从而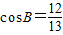 …(8分),
…(8分),
因为0<B<π,所以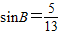 …(9分),
…(9分),
由正弦定理得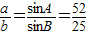 …(11分),所以,
…(11分),所以,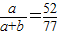 ,
, …(12分).
…(12分).
点评:本题主要考查两个向量的数量积公式,正弦定理以及正弦函数的定义域和值域,属于中档题.
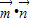 =4+sin2x,由
=4+sin2x,由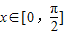 ,根据正弦函数的定义域和值域求得sin2x的范围,即可求得函数f(x)的值域.
,根据正弦函数的定义域和值域求得sin2x的范围,即可求得函数f(x)的值域.(2)由
 求得sinA的值;由
求得sinA的值;由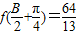 ,求得
,求得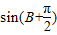 的值,从而求得cosB和sinB的值,再由正弦定理得
的值,从而求得cosB和sinB的值,再由正弦定理得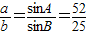 ,求得a的值.
,求得a的值.解答:解:(1)依题意,f(x)=
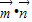 =2(2+sinxcosx)=4+sin2x…(3分),
=2(2+sinxcosx)=4+sin2x…(3分),由
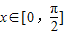 ,可得2x∈[0,π],sin2x∈[0,1],…(4分),
,可得2x∈[0,π],sin2x∈[0,1],…(4分),所以,函数f(x)在区间
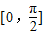 上的最大值为5.…(5分)
上的最大值为5.…(5分)(2)由
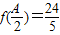 得
得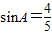 .…(6分),
.…(6分),由
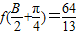 ,得
,得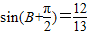 …(7分),从而
…(7分),从而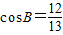 …(8分),
…(8分),因为0<B<π,所以
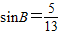 …(9分),
…(9分),由正弦定理得
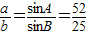 …(11分),所以,
…(11分),所以,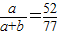 ,
, …(12分).
…(12分).点评:本题主要考查两个向量的数量积公式,正弦定理以及正弦函数的定义域和值域,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
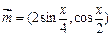 ,
, ,函数
,函数
 的最小正周期;
的最小正周期;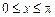 ,求
,求










 ,
, ,函数
,函数 .
. ,
, ,函数
,函数 .
. 在
在 上有解,求
上有解,求 的取值范围;
的取值范围; 中,
中, 分别是A,B,C所对的边,当(Ⅰ)中的
分别是A,B,C所对的边,当(Ⅰ)中的 时,求
时,求 的最小值.
的最小值. ,
, ,函数
,函数 .
. 的最小正周期以及单调递增区间;
的最小正周期以及单调递增区间; 时, 求
时, 求 在
在 内的所有实数根之和.
内的所有实数根之和.