题目内容
已知抛物线x2=y,O为坐标原点.(Ⅰ)过点O作两相互垂直的弦OM,ON,设M的横坐标为m,用n表示△OMN的面积,并求△OMN面积的最小值;
(Ⅱ)过抛物线上一点A(3,9)引圆x2+(y-2)2=1的两条切线AB,AC,分别交抛物线于点B,C,连接BC,求直线BC的斜率.
【答案】分析:(Ⅰ)由OM⊥ON,确定M,N的坐标,表示出|OM|= ,|ON|=
,|ON|=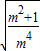 ,从而可得△OMN的面积,利用基本不等式可求△OMN面积的最小值;
,从而可得△OMN的面积,利用基本不等式可求△OMN面积的最小值;
(Ⅱ)设B( ),C(
),C( ),直线AB的方程为y-9=k1(x-3),AC的方程为y-9=k2(x-3),利用直线AB\AC与圆x2+(y-2)2=1相切,建立方程,从而可得以k1,k2 是方程4k2-21k+24=0的两根,再联立方程组,利用韦达定理,可得直线BC的斜率,化简可得结论.
),直线AB的方程为y-9=k1(x-3),AC的方程为y-9=k2(x-3),利用直线AB\AC与圆x2+(y-2)2=1相切,建立方程,从而可得以k1,k2 是方程4k2-21k+24=0的两根,再联立方程组,利用韦达定理,可得直线BC的斜率,化简可得结论.
解答:解:(Ⅰ)设M( ),N(
),N( ).
).
由OM⊥ON得 ,∴x1x2=-1.
,∴x1x2=-1.
因为x1=m,所以 .
.
所以|OM|=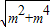 ,|ON|=
,|ON|= .
.
所以n= =
= ×
× ×
×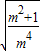 =
= =1.
=1.
所以,当m=1时,△OMN面积取得最小值1.
(Ⅱ)设B( ),C(
),C( ),直线AB的方程为y-9=k1(x-3),AC的方程为y-9=k2(x-3),
),直线AB的方程为y-9=k1(x-3),AC的方程为y-9=k2(x-3),
因为直线AB,AC与圆x2+(y-2)2=1相切,
所以 =
= =1.
=1.
所以 ,
, .
.
所以k1,k2 是方程4k2-21k+24=0的两根.
所以 .
.
由方程组 得x2-k1x-9+3k1=0.
得x2-k1x-9+3k1=0.
所以x3+3=k1,同理可得:x4+3=k2.
所以直线BC的斜率为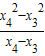 =x4+x3=k1+k2-6=-
=x4+x3=k1+k2-6=- .
.
点评:本题考查三角形面积的计算,考查基本不等式的运用,考查直线与圆,直线与抛物线的位置关系,考查韦达定理的运用,属于中档题.
 ,|ON|=
,|ON|=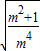 ,从而可得△OMN的面积,利用基本不等式可求△OMN面积的最小值;
,从而可得△OMN的面积,利用基本不等式可求△OMN面积的最小值;(Ⅱ)设B(
 ),C(
),C( ),直线AB的方程为y-9=k1(x-3),AC的方程为y-9=k2(x-3),利用直线AB\AC与圆x2+(y-2)2=1相切,建立方程,从而可得以k1,k2 是方程4k2-21k+24=0的两根,再联立方程组,利用韦达定理,可得直线BC的斜率,化简可得结论.
),直线AB的方程为y-9=k1(x-3),AC的方程为y-9=k2(x-3),利用直线AB\AC与圆x2+(y-2)2=1相切,建立方程,从而可得以k1,k2 是方程4k2-21k+24=0的两根,再联立方程组,利用韦达定理,可得直线BC的斜率,化简可得结论.解答:解:(Ⅰ)设M(
 ),N(
),N( ).
).由OM⊥ON得
 ,∴x1x2=-1.
,∴x1x2=-1.因为x1=m,所以
 .
.所以|OM|=
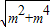 ,|ON|=
,|ON|= .
.所以n=
 =
= ×
× ×
×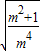 =
= =1.
=1.所以,当m=1时,△OMN面积取得最小值1.
(Ⅱ)设B(
 ),C(
),C( ),直线AB的方程为y-9=k1(x-3),AC的方程为y-9=k2(x-3),
),直线AB的方程为y-9=k1(x-3),AC的方程为y-9=k2(x-3),因为直线AB,AC与圆x2+(y-2)2=1相切,
所以
 =
= =1.
=1.所以
 ,
, .
.所以k1,k2 是方程4k2-21k+24=0的两根.
所以
 .
.由方程组
 得x2-k1x-9+3k1=0.
得x2-k1x-9+3k1=0.所以x3+3=k1,同理可得:x4+3=k2.
所以直线BC的斜率为
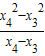 =x4+x3=k1+k2-6=-
=x4+x3=k1+k2-6=- .
.点评:本题考查三角形面积的计算,考查基本不等式的运用,考查直线与圆,直线与抛物线的位置关系,考查韦达定理的运用,属于中档题.

练习册系列答案
相关题目
已知抛物线x2=y,则它的准线方程为( )
A、x=
| ||
B、x=-
| ||
C、y=
| ||
D、y=-
|