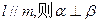题目内容
(本小题满分12分)
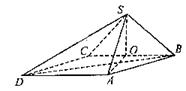
四棱锥S—ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD,已知
∠ABC = 45°AB=2,BC=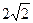 ,SA=SB =
,SA=SB =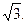
(Ⅰ)证明SA⊥BC;
(Ⅱ)求直线SD与平面SAB所成角的大小.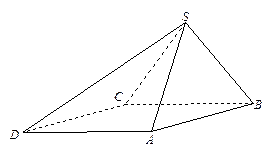
四棱锥S—ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD,已知
∠ABC = 45°AB=2,BC=
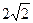 ,SA=SB =
,SA=SB =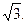
(Ⅰ)证明SA⊥BC;
(Ⅱ)求直线SD与平面SAB所成角的大小.

(Ⅰ)SA⊥BC
(Ⅱ)直线SD与平面SAB所成的角为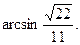
(Ⅱ)直线SD与平面SAB所成的角为
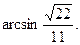
解法一:
(I)作SO⊥BC,垂足为O,连结AO,由侧面SBC⊥底面ABCD,得SO⊥底面ABCD.
因为SA=SB,所以AO=BO.
又∠ABC=45°,故△AOB为等腰直角三角形,AO⊥BO, 由三垂线定理,得SA⊥BC.
(II)由(I)知SA⊥BC,依题设AD∥BC,
故SA⊥AD,由AD=BC=2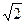 ,SA=
,SA=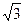 ,AO=
,AO=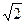 ,得
,得
SO=1,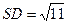 .
.
△SAB的面积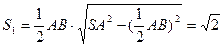 .
.
连结AB,得△DAB的面积 =2.
=2.
设D到平面SAB的距离为h,由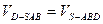 ,得
,得
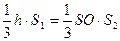 ,
,
解得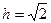 .
.
设SD与平面SAB所成角为α,则sinα=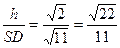 .
.
所以,直线SD与平面SAB所成的角为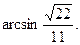
解法二:
(I)作SO⊥BC,垂足为O,连结AO,由侧面SBC⊥底面ABCD,得SO⊥平面ABCD.
因为SA=SB,所以AO=BO.
又∠ABC=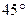 ,△AOB为等腰直角三角形,AO⊥OB.
,△AOB为等腰直角三角形,AO⊥OB.
如图,以O为坐标原点,OA为x轴正向,建立直角坐标系O—xyz,
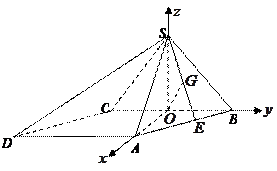 A(
A(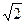 ,0,0),B(0,
,0,0),B(0,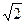 ,0),C(0,-
,0),C(0,-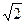 ,0),S(0,0,1),
,0),S(0,0,1),
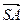 =(
=(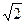 ,0,-1),
,0,-1),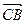 =(0,2
=(0,2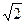 ,0),
,0),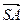 ·
·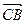 =0,
=0,
所以SA⊥BC.
(Ⅱ)取AB中点E,E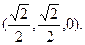
连结SE,取SE中点G,连结OG,G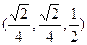 ,
,
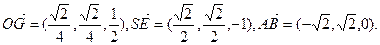
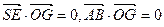 ,OG与平面SAB内两条相交直线SE,AB垂直,
,OG与平面SAB内两条相交直线SE,AB垂直,
所以OG⊥平面SAB.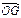 与
与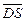 的夹角记为α,SD与平面SAB所成的角记为β,则α与β互余.
的夹角记为α,SD与平面SAB所成的角记为β,则α与β互余.
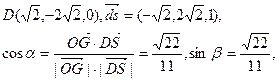
所以,直线SD与平面SAB所成的角为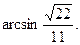
(I)作SO⊥BC,垂足为O,连结AO,由侧面SBC⊥底面ABCD,得SO⊥底面ABCD.
因为SA=SB,所以AO=BO.
|
(II)由(I)知SA⊥BC,依题设AD∥BC,
故SA⊥AD,由AD=BC=2
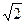 ,SA=
,SA=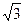 ,AO=
,AO=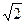 ,得
,得SO=1,
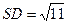 .
.△SAB的面积
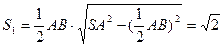 .
.连结AB,得△DAB的面积
 =2.
=2.设D到平面SAB的距离为h,由
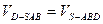 ,得
,得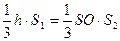 ,
,解得
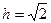 .
.设SD与平面SAB所成角为α,则sinα=
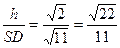 .
.所以,直线SD与平面SAB所成的角为
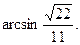
解法二:
(I)作SO⊥BC,垂足为O,连结AO,由侧面SBC⊥底面ABCD,得SO⊥平面ABCD.
因为SA=SB,所以AO=BO.
又∠ABC=
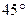 ,△AOB为等腰直角三角形,AO⊥OB.
,△AOB为等腰直角三角形,AO⊥OB.如图,以O为坐标原点,OA为x轴正向,建立直角坐标系O—xyz,
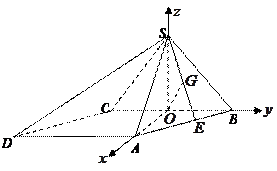 A(
A(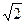 ,0,0),B(0,
,0,0),B(0,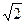 ,0),C(0,-
,0),C(0,-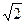 ,0),S(0,0,1),
,0),S(0,0,1),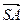 =(
=(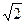 ,0,-1),
,0,-1),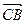 =(0,2
=(0,2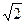 ,0),
,0),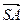 ·
·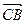 =0,
=0,所以SA⊥BC.
(Ⅱ)取AB中点E,E
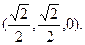
连结SE,取SE中点G,连结OG,G
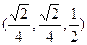 ,
,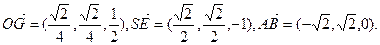
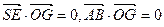 ,OG与平面SAB内两条相交直线SE,AB垂直,
,OG与平面SAB内两条相交直线SE,AB垂直,所以OG⊥平面SAB.
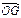 与
与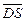 的夹角记为α,SD与平面SAB所成的角记为β,则α与β互余.
的夹角记为α,SD与平面SAB所成的角记为β,则α与β互余.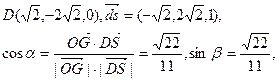
所以,直线SD与平面SAB所成的角为

练习册系列答案
相关题目

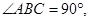
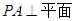 ,
,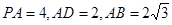 ,BC=6.
,BC=6.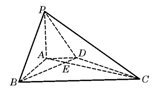
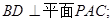
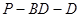 的大小.
的大小.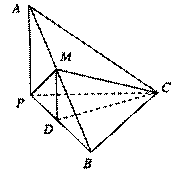
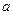 ,D为BC中点,M在BB1上,且
,D为BC中点,M在BB1上,且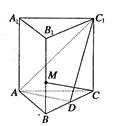
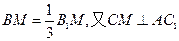 .
.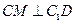 ;
;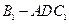 的体积.
的体积.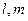 是两条不同的直线,
是两条不同的直线,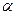 是一个平面,则下列命题错误的是 .
是一个平面,则下列命题错误的是 .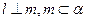 ,则
,则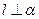 ;②若
;②若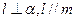 ,则
,则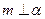 ;
;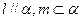 ,则
,则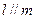 ;④若
;④若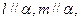 ,则
,则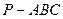 中,
中,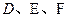 分别是
分别是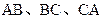 的中点,下面四个结论中不成立的是
的中点,下面四个结论中不成立的是 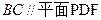
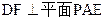
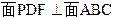
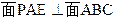
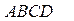 中,点
中,点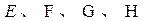 分别为
分别为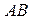 、
、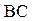 、
、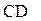 、
、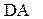 的中点,若
的中点,若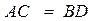 且
且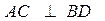 ,则四边形
,则四边形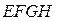 的具体形状为___________
的具体形状为___________
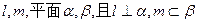 ,给出下列四个命题
,给出下列四个命题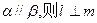 ;②若
;②若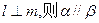 ;③若
;③若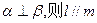 ;④若
;④若