题目内容
已知 为坐标原点,向量
为坐标原点,向量 ,
, ,点
,点 满足
满足 .
.
(1)记函数 ,讨论函数
,讨论函数 的单调性,并求其值域;
的单调性,并求其值域;
(2)若 三点共线,求
三点共线,求 的值.
的值.
【答案】
(1)增区间为 ,减区间为
,减区间为 ,值域为
,值域为 ;(2)
;(2)
【解析】本试题主要是考查了向量的数量积和模的运用。
解:(1) 设
设 ,则
,则 由
由 得
得
故 ………2分
………2分

 ………5分
………5分
又 故
故
当 即
即 时,
时, 单调递减;
单调递减;
当 即
即 时,
时, 单调递增.
单调递增.
故函数 的单调递增区间为
的单调递增区间为 ,单调递减区间为
,单调递减区间为 ,
………7分
,
………7分
因为 故函数
故函数 的值域为
的值域为 ………8分
………8分
(2) 由
由 三点共线可得
三点共线可得
 得
得 ,从而有 ………11分
,从而有 ………11分
 ………13分
………13分
 ………14分
………14分

练习册系列答案
相关题目
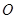 为坐标原点,向量
为坐标原点,向量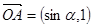 ,
,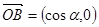 ,
,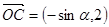 点
点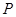 是直线
是直线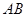 上一点,且
上一点,且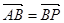 ;
;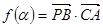 ,
, 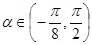 ,讨论
,讨论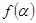 的单调性,并求其值域;
的单调性,并求其值域;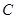 共线,求
共线,求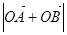 的值。
的值。