题目内容
已知 ,设
,设 ,
, ,
, ,那么a、b、c的大小关系是________.
,那么a、b、c的大小关系是________.
a≤b≤c
分析:化简a为 ,b为
,b为 ,c为
,c为 ,利用基本不等式可得
,利用基本不等式可得
 ≥
≥ ,用比较法可得
,用比较法可得  ≥
≥ .再由函数y=logsinθx是单调减函数可得a、b、c的大小关系.
.再由函数y=logsinθx是单调减函数可得a、b、c的大小关系.
解答:由题意可得 =
= ,
,
 =
= ,
,
 =
= .
.
∵θ∈( 0, ),∴1>sinθ>0,1>cosθ>0,∴
),∴1>sinθ>0,1>cosθ>0,∴ ≥
≥ ,
,
∴ ≤
≤ ,即 a≤b.
,即 a≤b.
∵ -
- =sinθcosθ-
=sinθcosθ- =
= =
=
= =
= ≥0,
≥0,
∴ ≥
≥ .
.
综上可得 ≥
≥ ≥
≥ .再由函数y=logsinθx是单调减函数可得,
.再由函数y=logsinθx是单调减函数可得,
a≤b≤c,
故答案为a≤b≤c.
点评:本题主要考查复合函数的单调性,基本不等式的应用,比较两个数大小的方法,属于中档题.
分析:化简a为
 ,b为
,b为 ,c为
,c为 ,利用基本不等式可得
,利用基本不等式可得  ≥
≥ ,用比较法可得
,用比较法可得  ≥
≥ .再由函数y=logsinθx是单调减函数可得a、b、c的大小关系.
.再由函数y=logsinθx是单调减函数可得a、b、c的大小关系.解答:由题意可得
 =
= ,
, =
= ,
, =
= .
.∵θ∈( 0,
 ),∴1>sinθ>0,1>cosθ>0,∴
),∴1>sinθ>0,1>cosθ>0,∴ ≥
≥ ,
,∴
 ≤
≤ ,即 a≤b.
,即 a≤b.∵
 -
- =sinθcosθ-
=sinθcosθ- =
= =
=
=
 =
= ≥0,
≥0,∴
 ≥
≥ .
.综上可得
 ≥
≥ ≥
≥ .再由函数y=logsinθx是单调减函数可得,
.再由函数y=logsinθx是单调减函数可得,a≤b≤c,
故答案为a≤b≤c.
点评:本题主要考查复合函数的单调性,基本不等式的应用,比较两个数大小的方法,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设f(x)为偶函数,对于任意的 ,都有f(2+x)=-2f(2-x),已知f(-1)=4,那么f(-3)等于
,都有f(2+x)=-2f(2-x),已知f(-1)=4,那么f(-3)等于
[ ]
|
A.2 |
B.-2 |
C.8 |
D.-8 |
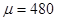 ,标准差
,标准差 ,总体服从正态分布,若云龙一中录取率为40%,那么云龙一中录取分数线可能划在(已知
,总体服从正态分布,若云龙一中录取率为40%,那么云龙一中录取分数线可能划在(已知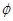 (0.25)=0.6) ( )
(0.25)=0.6) ( ) ,设
,设 ,
, ,
, ,那么a、b、c的大小关系是 .
,那么a、b、c的大小关系是 .