题目内容
(本题满分16分)
已知函数![]() 在
在![]() 是增函数,
是增函数,![]() 在(0,1)为减函数.
在(0,1)为减函数.
(Ⅰ)求![]() 、
、![]() 的表达式;
的表达式;
(Ⅱ)求证:当![]() 时,方程
时,方程![]() 有唯一解;
有唯一解;
(Ⅲ)当![]() 时,若
时,若![]() 在
在![]() ∈
∈![]() 内恒成立,求
内恒成立,求![]() 的取值范围.
的取值范围.
(本题满分16分)
解: (Ⅰ)![]() 依题意
依题意![]() 恒成立,
恒成立,
即![]() ,
,![]() 恒成立。 ∴
恒成立。 ∴![]() ① ………………………2分
① ………………………2分
又![]() ,依题意恒成立
,依题意恒成立![]() ,
,
即![]() ,
,![]() 恒成立。∴
恒成立。∴![]() ② …………………………4分
② …………………………4分
由①②得![]() .
.
∴![]() …………………………………5分
…………………………………5分
(Ⅱ)由(Ⅰ)可知,方程![]() ,
,![]()
设![]() ,
,
![]() ……………………7分
……………………7分
令![]() ,并由
,并由![]() 得
得![]()
列表分析:
|
| (0,1) | 1 | (1,+¥) |
|
| - | 0 | + |
|
| 递减 | 0 | 递增 |
知![]() 在
在![]() 处有一个最小值0, ……………………………9分
处有一个最小值0, ……………………………9分
∴当![]() 时,
时,![]() >0, ∴
>0, ∴![]() 在(0,+¥)上只有一个解.
在(0,+¥)上只有一个解.
即当x>0时,方程![]() 有唯一解。 ……………………………11分
有唯一解。 ……………………………11分
(Ⅲ)![]() 在
在![]() ∈
∈![]() 恒成立
恒成立![]()
![]() 在
在![]() ∈
∈![]() 内恒成立
内恒成立
![]() 在
在![]() ∈
∈![]() 内恒成立…③ …………………………13分
内恒成立…③ …………………………13分
令![]() (
(![]() ∈
∈![]() ),
),
则![]()
![]() ∈
∈![]() 时,
时,![]() ,
,![]() 在
在![]() 是减函数,
是减函数,![]()
由③知![]() ,
,![]() …………………………………15分
…………………………………15分
又![]() ,所以:
,所以:![]() 为所求范围. …………………………………16分
为所求范围. …………………………………16分
另解:设![]() , 则
, 则![]() 时,
时,
![]() 13分
13分
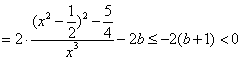 ……………………15分
……………………15分
![]() 在
在![]() 为减函数,
为减函数,![]() ,
,![]()
又![]() ,所以:
,所以:![]() 为所求范围. …………………………16分
为所求范围. …………………………16分

练习册系列答案
相关题目


 在
在 上的单调性;
上的单调性; ,使
,使 ,则称
,则称 的不动点,现已知该函数有且仅有一个不动点,求
的不动点,现已知该函数有且仅有一个不动点,求 的值;
的值; 在
在