题目内容
(2013•湖南模拟)已知双曲线
-
=1的一个焦点与抛物线y2=4
x的焦点重合,且双曲线的离心率等于
,则该双曲线的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 10 |
| ||
| 3 |
分析:求出抛物线的焦点坐标,利用双曲线的一个焦点与抛物线y2=4
x的焦点重合,且双曲线的离心率等于
,建立方程组,求出几何量,即可求得双曲线的标准方程.
| 10 |
| ||
| 3 |
解答:解:抛线线y2=4
x的焦点(
,0)
∴c2=a2+b2=10,e=
=
.
∴a=3,b=1,
∴该双曲线的方程为
-y2=1.
故选C.
| 10 |
| 10 |
∴c2=a2+b2=10,e=
| ||
| a |
| ||
| 3 |
∴a=3,b=1,
∴该双曲线的方程为
| x2 |
| 9 |
故选C.
点评:本题考查抛物线的性质,考查双曲线的标准方程,考查学生的计算能力,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2013•湖南模拟)设椭圆
(2013•湖南模拟)设椭圆 (2013•湖南模拟)如图所示,已知△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,tan∠EAB=
(2013•湖南模拟)如图所示,已知△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,tan∠EAB=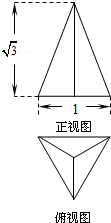 (2013•湖南模拟)已知三棱锥的底面是边长为1的正三角形,其正视图与俯视图如图所示,则其侧视图的面积为( )
(2013•湖南模拟)已知三棱锥的底面是边长为1的正三角形,其正视图与俯视图如图所示,则其侧视图的面积为( ) (2013•湖南模拟)已知集合M={x∈Z|-1≤x≤1},N={x∈Z|x(x-2)≤0},则如图所示韦恩图中的阴影部分所表示的集合为( )
(2013•湖南模拟)已知集合M={x∈Z|-1≤x≤1},N={x∈Z|x(x-2)≤0},则如图所示韦恩图中的阴影部分所表示的集合为( )