题目内容
对某电子元件进行寿命追踪调查,所得情况如下频率分布直方图.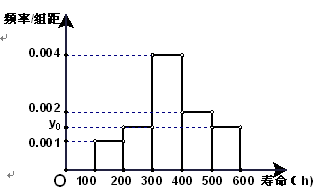
(1)图中纵坐标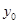 处刻度不清,根据图表所提供的数据还原
处刻度不清,根据图表所提供的数据还原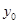 ;
;
(2)根据图表的数据按分层抽样,抽取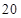 个元件,寿命为
个元件,寿命为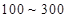 之间的应抽取几个;
之间的应抽取几个;
(3)从(2)中抽出的寿命落在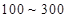 之间的元件中任取
之间的元件中任取 个元件,求事件“恰好有一个寿命为
个元件,求事件“恰好有一个寿命为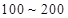 ,一个寿命为
,一个寿命为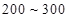 ”的概率.
”的概率.
(1)0.0015 (2)5 (3)
解析试题分析:(1)根据频率直方图的意义可知所有小矩形的面积之和等于1,列出关于y0的方程求解即可.
(2)根据频数= ×组距求解即可.
×组距求解即可.
(3)用列举法写出从寿命为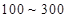 之间的5个元件中任取2个的所有结果及总数,在找出“恰好有一个寿命为
之间的5个元件中任取2个的所有结果及总数,在找出“恰好有一个寿命为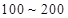 ,一个寿命为
,一个寿命为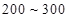 ”的所有结果及个数,最后根据随机事件的概率公式求解.
”的所有结果及个数,最后根据随机事件的概率公式求解.
试题解析:解(1)根据题意:
解得 3分
3分
(2)设在寿命为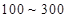 之间的应抽取
之间的应抽取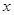 个,根据分层抽样有:
个,根据分层抽样有: 5分
5分
解得:
所以应在寿命为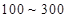 之间的应抽取
之间的应抽取 个 7分
个 7分
(3)记“恰好有一个寿命为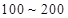 ,一个寿命为
,一个寿命为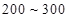 ”为事件
”为事件 ,由(2)知寿命落在
,由(2)知寿命落在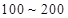 之间的元件有
之间的元件有 个分别记
个分别记 ,落在
,落在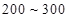 之间的元件有
之间的元件有 个分别记为:
个分别记为: ,从中任取
,从中任取 个球,有如下基本事件:
个球,有如下基本事件:
 ,
, ,共有
,共有 个基本事件 9分
个基本事件 9分
事件 “恰好有一个寿命为
“恰好有一个寿命为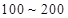 ,一个寿命为
,一个寿命为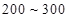 ”有:
”有: ,
, 共有
共有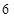 个基本事件 10分
个基本事件 10分 11分
11分
答:事件“恰好有一个寿命为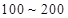 ,另一个寿命为
,另一个寿命为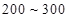 ”的概率为
”的概率为 12分
12分
考点:1.数据频率分布直方图;2.随机事件的概率.

某工厂生产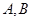 两种元件,其质量按测试指标划分为:大于或等于7.5为正品,小于7.5为次品.现从一批产品中随机抽取这两种元件各5件进行检测,检测结果记录如下:
两种元件,其质量按测试指标划分为:大于或等于7.5为正品,小于7.5为次品.现从一批产品中随机抽取这两种元件各5件进行检测,检测结果记录如下:
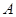 | 7 | 7 | 7.5 | 9 | 9.5 |
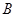 | 6 | 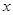 | 8.5 | 8.5 |  |
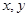 看不清,统计员只记得
看不清,统计员只记得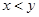 ,且
,且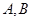 两种元件的检测数据的平均值相等,方差也相等.
两种元件的检测数据的平均值相等,方差也相等.(Ⅰ)求表格中
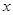 与
与 的值;
的值;(Ⅱ)若从被检测的5件
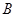 种元件中任取2件,求2件都为正品的概率.
种元件中任取2件,求2件都为正品的概率. 某学校的三个学生社团的人数分布如下表(每名学生只能参加一个社团):
| | 围棋社 | 舞蹈社 | 拳击社 |
| 男生 | 5 | 10 | 28 |
| 女生 | 15 | 30 | m |
(Ⅰ)求拳击社女生有多少人;
(Ⅱ)从围棋社指定的3名男生和2名女生中随机选出2人参加围棋比赛,求这两名同学是一名男生和一名女生的概率.
在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人。女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动。
(Ⅰ)根据以上数据建立一个2×2列联表;
(Ⅱ)试判断是否有97.5%的把握认为“休闲方式与性别有关”?
下面临界值表仅供参考:
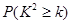 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
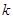 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
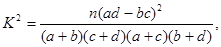 其中
其中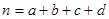 )
) 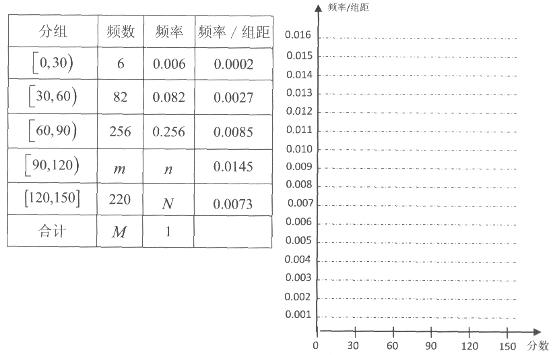
 是指大气中直径小于或等于
是指大气中直径小于或等于 微米的颗粒物,也称为可吸入肺颗粒物.我国
微米的颗粒物,也称为可吸入肺颗粒物.我国 微克/立方米以下空气质量为一级;在
微克/立方米以下空气质量为一级;在 微克/立方米之间空气质量为二级;在
微克/立方米之间空气质量为二级;在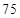 微克/立方米以上空气质量为超标.某试点城市环保局从该市市区
微克/立方米以上空气质量为超标.某试点城市环保局从该市市区 年上半年每天的
年上半年每天的 天的数据作为样本,监测值如下图茎叶图所示(十位为茎,个位为叶).
天的数据作为样本,监测值如下图茎叶图所示(十位为茎,个位为叶).
 天数据,记
天数据,记 表示抽到
表示抽到 天计算)中平均有多少天的空气质量达到一级或二级.
天计算)中平均有多少天的空气质量达到一级或二级.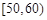 ,
,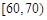 ,
,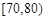 ,
,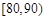 ,
,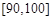 的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在
的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在
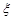 表示所抽取的3名同学中得分在
表示所抽取的3名同学中得分在