题目内容
【题目】如图，圆O是△ABC的外接圆，∠BAC的平分线交BC于点F，D是AF的延长线与⊙O的交点，AC的延线与⊙O的切线DE交于点E．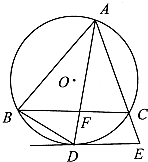 
（1）求证： 
= 
（2）若BD=3 
，EC=2，CA=6，求BF的值．
【答案】
（1）证明：连接CD，则
∵AD平分∠BAC，
∴∠BAD=∠EAD， 
= 
，
∵DE是圆O的切线，
∴∠CDE=∠EAD=∠BAD．
∵∠DCE是四边形ABCD的外角，
∴∠DCE=∠ABD，
∴△ABD∽△DCE，
∴ 
= 
．
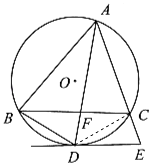
（2）解：∵ = ，BD=3 
，
∴BD=CD=3 ，∠CBD=∠BCD，
∵DE是圆O的切线，EC=2，CA=6，
∴∠CDE=∠CBD，DE2=ECEA=16，
∴DE=4，
∴∠CDE=∠BCD，
∴DE∥BC，
∴∠E=∠ACB=∠ADB，
∴△DCE∽△BFD，
∴ 
，
∴BF= 
= 
【解析】（1）连接CD，证明△ABD∽△DCE，即可证明： = （2）若BD=3 ，EC=2，CA=6，求出DE，证明△DCE∽△BFD，即可求BF的值．
练习册系列答案
相关题目
