题目内容
已知函数y=ax2+b|x|+c(a≠0)在其定义域内有四个单调区间,且a,b,c∈{-2,-1,0,1,2,3,4},在这些函数中,设随机变量ξ=“|a-b|的取值”,则ξ的数学期望Eξ为
- A.4
- B.
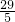
- C.

- D.

A
分析:要使函数在R上有四个单调区间,则在(-∞,0)和[0,+∞)内各有两个单调区间,据此利用组合数公式求得抛物线条数,写出ξ分布列即可.
解答:函数y=ax2+b|x|+c(a≠0)在其定义域R内是偶函数,
关于y轴对称,且 ,
,
要使函数在R上有四个单调区间,则在(-∞,0)和[0,+∞)内各有两个单调区间,
故 即对称轴在y轴右侧,这样的抛物线有2 C21C41C71=112条,由ξ=|a-b|,
即对称轴在y轴右侧,这样的抛物线有2 C21C41C71=112条,由ξ=|a-b|,
可知ξ可取的值有2,3,4,5,6,得 ,
, ,
, ,
, ,
, ,
, =
= ,
,
故选A.
点评:本题考查圆锥曲线、排列组合与概率统计的综合应用.本题关键是懂得利用组合数公式求得抛物线条数,写出ξ分布列即可.
分析:要使函数在R上有四个单调区间,则在(-∞,0)和[0,+∞)内各有两个单调区间,据此利用组合数公式求得抛物线条数,写出ξ分布列即可.
解答:函数y=ax2+b|x|+c(a≠0)在其定义域R内是偶函数,
关于y轴对称,且
 ,
,要使函数在R上有四个单调区间,则在(-∞,0)和[0,+∞)内各有两个单调区间,
故
 即对称轴在y轴右侧,这样的抛物线有2 C21C41C71=112条,由ξ=|a-b|,
即对称轴在y轴右侧,这样的抛物线有2 C21C41C71=112条,由ξ=|a-b|,可知ξ可取的值有2,3,4,5,6,得
 ,
, ,
, ,
, ,
, ,
, =
= ,
,故选A.
点评:本题考查圆锥曲线、排列组合与概率统计的综合应用.本题关键是懂得利用组合数公式求得抛物线条数,写出ξ分布列即可.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目