题目内容
已知正项等比数列{an}满足:a3=a2+2a1,若存在两项am,an,使得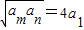 ,则
,则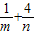 的最小值为( )
的最小值为( )A.

B.

C.
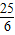
D.不存在
【答案】分析:由正项等比数列{an}满足:a3=a2+2a1,知q=2,由存在两项am,an,使得 ,知m+n=6,由此能求出
,知m+n=6,由此能求出 的最小值.
的最小值.
解答:解:∵正项等比数列{an}满足:a3=a2+2a1,
∴ ,
,
即:q2=q+2,解得q=-1(舍),或q=2,
∵存在两项am,an,使得 ,
,
∴ ,
,
∴ ,
,
∴ ,
,
所以,m+n=6,
∴ =(
=( )[
)[ (m+n)]=
(m+n)]= (5+
(5+ +
+ )≥
)≥ (5+2
(5+2 )=
)= ,
,
所以, 的最小值是
的最小值是 .
.
点评:本题考查等比数列的通项公式的应用,解题时要认真审题,仔细解答.注意不等式也是高考的热点,尤其是均值不等式和一元二次不等式的考查,两者都兼顾到了.
 ,知m+n=6,由此能求出
,知m+n=6,由此能求出 的最小值.
的最小值.解答:解:∵正项等比数列{an}满足:a3=a2+2a1,
∴
 ,
,即:q2=q+2,解得q=-1(舍),或q=2,
∵存在两项am,an,使得
 ,
,∴
 ,
,∴
 ,
,∴
 ,
,所以,m+n=6,
∴
 =(
=( )[
)[ (m+n)]=
(m+n)]= (5+
(5+ +
+ )≥
)≥ (5+2
(5+2 )=
)= ,
,所以,
 的最小值是
的最小值是 .
.点评:本题考查等比数列的通项公式的应用,解题时要认真审题,仔细解答.注意不等式也是高考的热点,尤其是均值不等式和一元二次不等式的考查,两者都兼顾到了.

练习册系列答案
相关题目
已知正项等比数列{an}中,a1=1,a3a7=4a62,则S6=( )
A、
| ||
B、
| ||
C、
| ||
| D、2 |
已知正项等比数列{an}满足:a7=a6+2a5,若存在两项am,an使得
=4a1,则
+
的最小值为( )
| aman |
| 1 |
| m |
| 1 |
| n |
A、
| ||
B、
| ||
C、
| ||
| D、不存在 |
已知正项等比数列{an}的前n项和为Sn,若S3=3,S9-S6=12,则S6=( )
| A、9 | ||
B、
| ||
| C、18 | ||
| D、39 |