题目内容

已知点P(1,-1),直线l的方程为x-2y+1=0.求经过点P,且倾斜角为直线l的倾斜角一半的直线方程.

解：设直线l的倾斜角为α,则所求直线的倾斜角为,由已知直线l的斜率为tanα=及公式tanα=,得

    tan2+2·tan-1=0.

    解得tan=-或tan=--.

    由于tanα=,而0＜＜1,故0＜α＜,0＜＜.因此tan＞0.

    于是所求直线的斜率为k=tan=-.

   故所求的直线方程为y-(-1)=(-)(x-1),

    即(-)x-y-(-+1)=0.

练习册系列答案
相关题目
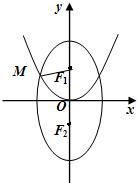精英家教网与向量、圆交汇．例5：已知F1、F2分别为椭圆C1：
y2
a2
+
x2
b2
=1(a＞b＞0)的上、下焦点，其中F1也是抛物线C2：x2=4y的焦点，点M是C1与C2在第二象限的交点，且|MF1|=
5
3
．
（1）求椭圆C1的方程；
（2）已知点P（1，3）和圆O：x2+y2=b2，过点P的动直线l与圆O相交于不同的两点A，B，在线段AB上取一点Q，满足：
AP
=-λ
PB
，
AQ
=λ
QB
，（λ≠0且λ≠±1）．问点Q是否总在某一定直线上？若在，求出这条直线，否则，说明理由．
已知点F是双曲线C：x2-y2=2的左焦点，直线l与双曲线C交于A、B两点，
（1）若直线l过点P（1，2），且
OA
+
OB
=2
OP
，求直线l的方程．
（2）若直线l过点F且与双曲线的左右两支分别交于A、B两点，设
FB
=λ
FA
，当λ∈[6，+∞）时，求直线l的斜率k的取值范围．
如图，已知F1、F2分别为椭圆C1：
y2
a2
+
x2
b2
=1(a＞b＞0)的上、下焦点，其中F1也是抛物线C2：x2=4y的焦点，点M是C1与C2在第二象限的交点，且|MF1|=
5
3
．
（1）求椭圆C1的方程；
（2）已知点P（1，3）和圆O：x2+y2=b2，过点P的动直线l与圆O相交于不同的两点A，B，在线段AB上取一点Q，满足：
AP
=-λ
PB
，
AQ
=λ
QB
（λ≠0且λ≠±1），
求证：点Q总在某条定直线上．
已知点P的柱坐标为(,,5)，点B的球坐标为(,,)，则这两个点在空间直角坐标系中的点的坐标为(    )

A.P点(5,1,1)，B点()

B.P点(1,1,5)，B点()

C.P点()，B点(1,1,5)

D.P点(1,1,5)，B点()

已知点P(1,-1),F为椭圆+=1的右焦点,M为椭圆上一点,且使|MP|+2|MF|的值最小,则点M为______________.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网