题目内容
等比数列{an}的前3项的和等于首项的3倍,则它的公比为( )
| A.-2 | B.1 | C.-2或1 | D.2或-1 |
C
解析试题分析:当公比为1时,显然S3=3a1,当公比不为1时,那么根据等比数列的前n项和公式可知,
S3= ,故有
,故有 ,故选C
,故选C
考点:本试题主要考查了等比数列的通项公式和前n项和的求解运用。
点评:解决该试题的关键是对于公比是否为1,要注意讨论。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设等比数列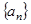 中,前n项和为
中,前n项和为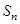 ,已知
,已知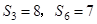 ,则
,则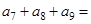
A. | B.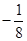 | C.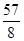 | D.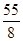 |
在等比数列{an}中, =1,
=1, =3,则
=3,则 的值是
的值是
| A.14 | B.16 | C.18 | D.20 |
记等比数列 的前
的前 项和为
项和为 ,若
,若 则
则 ( )
( )
| A. 9 | B.27 | C. 8 8 | D.8 |
等比数列 中,首项
中,首项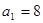 ,公比
,公比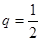 ,那么
,那么 前5项和
前5项和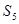 的值是
的值是
A.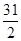 | B.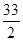 | C.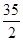 | D.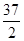 |
已知 是等比数列,
是等比数列, ,则公比
,则公比 =( )
=( )
A. | B. | C.2 | D. |
数列1,1+2,1+2+22,…,1+2+22+…+2n-1,…的前n项和为( )
| A.2n-n-1 | B.2n+1-n-2 |
| C.2n | D.2n+1-n |
已知{an}是等比数列, ,则公比q=( )
,则公比q=( )
A. | B.-2 | C.2 | D. |
 的左右焦点分别为
的左右焦点分别为 ,P是椭圆上的一点,且
,P是椭圆上的一点,且 成等比数列,则椭圆的离心率的取值范围为( )
成等比数列,则椭圆的离心率的取值范围为( )


