题目内容
讨论函数y=(
)
的单调性.
解法一:因为函数的定义域为(－∞,+∞),设x1、x2∈(－∞,+∞),且x1＜x2,
所以f(x1)=(),f(x2)=(
)
,
=
=(
)
=(
)
.
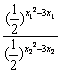当x1＜x2≤
时,x1+x2＜3,
即有x1+x2－3＜0.
又因为x1－x2＜0,所以(x1－x2)(x1+x2－3)＞0,
(
)
＜1.
又对于x∈R,f(x)＞0恒成立,
所以f(x1)＜f(x2).
所以函数f(x)在(－∞,
］上单调递增.
同理,
≤x1＜x2时,有f(x1)＞f(x2).
所以函数f(x)在［
,+∞)上单调递减.
解法二:函数的定义域为R,令u=x2－3x,则y=(
)u.
因为u=x2－3x=(x－
)2－
在［
,+∞)上是增函数,在(－∞,
］上是减函数,而y=(
)u在定义域内是减函数,所以函数y=(
)
在［
,+∞)上为减函数,在(－∞,
］上为增函数.
点评:对于指数函数的复合函数的单调性的证明问题仍然用定义法,即“取值——作差 ——变形——定号”.其中在定号过程中需要用到指数函数的单调性.对于其单调性的判断,一般用复合法,但应注意中间变量的取值范围.
练习册系列答案
相关题目
+b(x≠0)，其中a，b∈R，
，2]，不等式f(x)≤10在[
，1]上恒成立，求b的取值范围。 
+b(x≠0),其中a,b∈R.
,2］,不等式f(x)≤10在［
,1］上恒成立,求b的取值范围.
对称，且f′(1)＝0.