题目内容
如图，正方体ABCD—A1B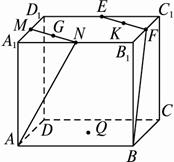
证明：引进坐标系(D为原点,射线DA、DC、DD1分别为x、y、z轴正方向)，则A(4,0,0),M(2,0,4),N(4,2,4),D(0,0,0),B(4,4,0),E(0,2,4),F(2,4,4).?
取MN的中点G及EF的中点K，BD的中点Q，则G(3,1,4),K(1,3,4),Q(2,2,0).?
∴
=(2,2,0),
=(2,2,0),
=(-1,1,4),
=(-1,1,4).?
可见
=
，
=
,?
∴MN∥EF,AG∥QK.?
∴MN∥平面EFBD，AG∥平面EFBD.?
∴平面AMN∥平面EFBD.
练习册系列答案
名师导航单元期末冲刺100分系列答案
名校名卷单元同步训练测试题系列答案
相关题目
如图，正方体ABCD-A1B1C1D1中，E，F分别为BB1和A1D1的中点．证明：向量
如图，正方体ABCD-A1B1C1D1棱长为8，E、F分别为AD1，CD1中点，G、H分别为棱DA，DC上动点，且EH⊥FG．
如图，正方体ABCD-A1B1C1D1中，若E、F、G分别为棱BC、C1C、B1C1的中点，O1、O2分别为四边形ADD1A1、A1B1C1D1的中心，则下列各组中的四个点不在同一个平面上的是（ ）
如图，正方体ABCD-A1B1C1D1中，E、F、G、H分别是所在棱的三等分点，且