题目内容
已知正方形ABCD,则以A、B为焦点,且过C、D两点的椭圆的离心率为分析:由“以A、B为焦点”可求得c,再由“过C、D两点”结合椭圆的定义可知|AC|+|BC|=2a,可求a,再由离心率公式求得其离心率.
解答:解:设正方形边长为1,则AB=2c=1,
∴c=
.
∵|AC|+|BC|=1+
=2a,
∴a=
.
∴e=
=
=
-1.
故答案为:
-1
∴c=
| 1 |
| 2 |
∵|AC|+|BC|=1+
| 2 |
∴a=
| ||
| 2 |
∴e=
| c |
| a |
| ||||
|
| 2 |
故答案为:
| 2 |
点评:本题通过正方形来构造椭圆,来考查其定义及性质,题目灵活新颖,转化巧妙,是一道好题.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
已知正方形ABCD边长为1,则|
+
+
|=( )
| AB |
| BC |
| AC |
| A、0 | ||
| B、2 | ||
C、
| ||
D、2
|
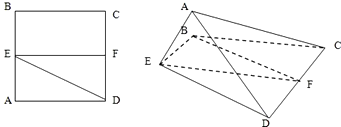 已知正方形ABCD.E、F分别是AB、CD的中点,将△ADE沿DE折起,如图所示,记二面角A-DE-C的大小为θ(0<θ<π).
已知正方形ABCD.E、F分别是AB、CD的中点,将△ADE沿DE折起,如图所示,记二面角A-DE-C的大小为θ(0<θ<π). (2008•虹口区二模)(理)已知正方形ABCD的边长为1,PD⊥平面ABCD,PD=3,
(2008•虹口区二模)(理)已知正方形ABCD的边长为1,PD⊥平面ABCD,PD=3,