题目内容
14.在等比数列{an}中,(1)若已知a2=4,a5=-$\frac{1}{2}$,求an;
(2)若已知a3a4a5=8,求a2a6的值.
分析 (1)设等比数列{an}的公比为q,由等比数列的通项公式可得q=-$\frac{1}{2}$,可得通项公式;
(2)由等比数列的性质和已知可得a4=2,代入a2a6=a42可得.
解答 解:(1)设等比数列{an}的公比为q,
则q3=$\frac{{a}_{5}}{{a}_{2}}$=$-\frac{1}{8}$,解得q=-$\frac{1}{2}$,
∴an=4×(-$\frac{1}{2}$)n-2=(-$\frac{1}{2}$)n-4;
(2)由等比数列的性质可得a3a4a5=a43=8,
∴a4=2,∴a2a6=a42=4.
点评 本题考查等比数列的通项公式,属基础题.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
4.已知定义在R上的函数$f(x)={(\frac{1}{2})^{|x-m|}}-1$(m为实数)为偶函数,记a=f(log0.53),b=f(log25),c=f(2m),则a,b,c的大小关系为( )
| A. | a<b<c | B. | b<a<c | C. | c<a<b | D. | a<c<b |
2.已知点A(-3,8),B(2,2),点P是x轴上的点,则当|AP|+|PB|最小时点P的坐标( )
| A. | (1,0) | B. | ($\frac{1}{2}$,0) | C. | ($\frac{1}{3}$,0) | D. | ($\frac{1}{4}$,0) |
4. 结晶体的基本单位称为晶胞,如图是食盐晶胞的示意图(可看成是八个棱长为$\frac{1}{2}$的小正方体堆积成的正方体).其中实圆•代表钠原子,空间圆?代表氯原子.建立空间直角坐标系Oxyz后,图中最上层中间的钠原子所在位置的坐标是( )
结晶体的基本单位称为晶胞,如图是食盐晶胞的示意图(可看成是八个棱长为$\frac{1}{2}$的小正方体堆积成的正方体).其中实圆•代表钠原子,空间圆?代表氯原子.建立空间直角坐标系Oxyz后,图中最上层中间的钠原子所在位置的坐标是( )
 结晶体的基本单位称为晶胞,如图是食盐晶胞的示意图(可看成是八个棱长为$\frac{1}{2}$的小正方体堆积成的正方体).其中实圆•代表钠原子,空间圆?代表氯原子.建立空间直角坐标系Oxyz后,图中最上层中间的钠原子所在位置的坐标是( )
结晶体的基本单位称为晶胞,如图是食盐晶胞的示意图(可看成是八个棱长为$\frac{1}{2}$的小正方体堆积成的正方体).其中实圆•代表钠原子,空间圆?代表氯原子.建立空间直角坐标系Oxyz后,图中最上层中间的钠原子所在位置的坐标是( )| A. | ($\frac{1}{2}$,$\frac{1}{2}$,1) | B. | (0,0,1) | C. | (1,$\frac{1}{2}$,1) | D. | (1,$\frac{1}{2}$,$\frac{1}{2}$) |
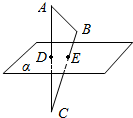 如图所示,D、E分别是△ABC的边AC、BC上的点,平面α经过D、E两点.
如图所示,D、E分别是△ABC的边AC、BC上的点,平面α经过D、E两点.