题目内容
已知动点C(x,y)到点A(-1,0)的距离是它到点B(1,0)的距离的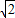 倍.
倍.(Ⅰ) 试求点C的轨迹方程;
(Ⅱ) 试用你探究到的结果求△ABC面积的最大值.
【答案】分析:(Ⅰ)根据点到点的距离公式,再进行化简后可得;
(Ⅱ)现在要使面积最大,即点C的Y坐标的绝对值最大,故可求.
解答:解:(Ⅰ)由题意, ,即
,即 ,∴(x-3)2+y2=8….(8分)
,∴(x-3)2+y2=8….(8分)
(Ⅱ)由(Ⅰ)知,轨迹为圆心为(3,0)半径为 的圆,而三角形ABC的AB边长为2,现在要使面积最大,即点C的Y坐标的绝对值最大,很容易求出C的Y坐标的绝对值最大为
的圆,而三角形ABC的AB边长为2,现在要使面积最大,即点C的Y坐标的绝对值最大,很容易求出C的Y坐标的绝对值最大为 (即为半径),∴
(即为半径),∴ ….(10分)
….(10分)
∴ ….(15分)
….(15分)
点评:本题主要考查轨迹方程的求法及利用方程解决面积的最大值问题.
(Ⅱ)现在要使面积最大,即点C的Y坐标的绝对值最大,故可求.
解答:解:(Ⅰ)由题意,
 ,即
,即 ,∴(x-3)2+y2=8….(8分)
,∴(x-3)2+y2=8….(8分)(Ⅱ)由(Ⅰ)知,轨迹为圆心为(3,0)半径为
 的圆,而三角形ABC的AB边长为2,现在要使面积最大,即点C的Y坐标的绝对值最大,很容易求出C的Y坐标的绝对值最大为
的圆,而三角形ABC的AB边长为2,现在要使面积最大,即点C的Y坐标的绝对值最大,很容易求出C的Y坐标的绝对值最大为 (即为半径),∴
(即为半径),∴ ….(10分)
….(10分)∴
 ….(15分)
….(15分)点评:本题主要考查轨迹方程的求法及利用方程解决面积的最大值问题.

练习册系列答案
相关题目
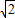 倍.
倍.