题目内容
已知x∈[0,1],函数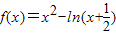 ,g(x)=x3-3a2x-4a.
,g(x)=x3-3a2x-4a.(1)求f(x)的单调区间和值域;
(2)设a≤-1,若?x1∈[0,1],总?x∈[0,1],使得g(x)=f(x1)成立,求a的取值范围;
(3)对于任意的正整数n,证明
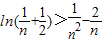 -1.(注:
-1.(注: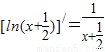 )
)
【答案】分析:(1)令f′(x)=0可得极值点,列出随x变化时f′(x),f(x)的变化表,由表可知单调区间,根据单调性可得最值,进而得到值域;
(2)利用导数可判断g(x)在[0,1]上的单调性,从而可求值域为[1-4a-3a2,-4a],由题意,得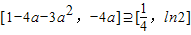 ,由此可得不等式组,解出即可;
,由此可得不等式组,解出即可;
(3)构造函数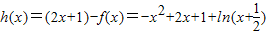 ,利用导数可判断h(x)在[0,1]上的单调性,根据单调性可证h(x)>h(0)>0,整理该不等式后令x=
,利用导数可判断h(x)在[0,1]上的单调性,根据单调性可证h(x)>h(0)>0,整理该不等式后令x=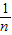 即可;
即可;
解答:解:(1)令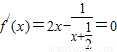 ,解得
,解得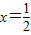 ,x=-1舍去.
,x=-1舍去.
由下表:
可知,f(x)的单调递减区间是(0, ),递增区间是(
),递增区间是( ,1);
,1);
f(x)在 处取得极小值,也为最小值,
处取得极小值,也为最小值,
又 =
=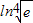 <
<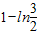 =
=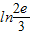 <ln2,
<ln2,
故当x∈[0,1]时,f(x)的值域为[ ,ln2];
,ln2];
(2)∵g'(x)=3(x2-a2),
∴当a≤-1,x∈(0,1)时,g'(x)<3(1-a2)≤0,
∴g(x)为[0,1]上的减函数,从而当x∈[0,1]时有g(x)∈[g(1),g(0)]=[1-4a-3a2,-4a].
由题意,得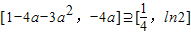 ,
,
即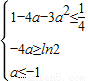 ,解得a
,解得a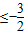 ,
,
故a的取值范围为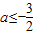 .
.
(3)构造函数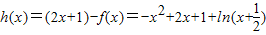 ,
,
则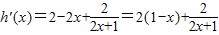 ,
,
当x∈[0,1]时,h′(x)>0,∴函数h(x)在[0,1]上单调递增,
又h(0)=1-ln2>0,
∴x∈[0,1]时,恒有h(x)>h(0)>0,即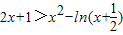 恒成立,
恒成立,
故对任意正整数n,取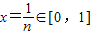 ,有
,有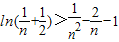 .
.
点评:本题考查利用导数研究函数的单调性、函数的最值,考查转化思想,考查学生分析问题解决问题的能力,解决(3)问的关键是根据目标式恰当构造函数.
(2)利用导数可判断g(x)在[0,1]上的单调性,从而可求值域为[1-4a-3a2,-4a],由题意,得
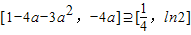 ,由此可得不等式组,解出即可;
,由此可得不等式组,解出即可;(3)构造函数
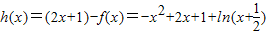 ,利用导数可判断h(x)在[0,1]上的单调性,根据单调性可证h(x)>h(0)>0,整理该不等式后令x=
,利用导数可判断h(x)在[0,1]上的单调性,根据单调性可证h(x)>h(0)>0,整理该不等式后令x=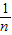 即可;
即可;解答:解:(1)令
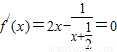 ,解得
,解得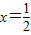 ,x=-1舍去.
,x=-1舍去.由下表:
| x | (0, ) ) |  | ( ,1) ,1) | 1 | |
| f'(x) | - | + | |||
| f(x) | ln2 |  | 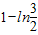 |
 ),递增区间是(
),递增区间是( ,1);
,1); f(x)在
 处取得极小值,也为最小值,
处取得极小值,也为最小值,又
 =
=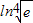 <
<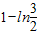 =
=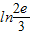 <ln2,
<ln2,故当x∈[0,1]时,f(x)的值域为[
 ,ln2];
,ln2];(2)∵g'(x)=3(x2-a2),
∴当a≤-1,x∈(0,1)时,g'(x)<3(1-a2)≤0,
∴g(x)为[0,1]上的减函数,从而当x∈[0,1]时有g(x)∈[g(1),g(0)]=[1-4a-3a2,-4a].
由题意,得
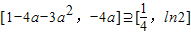 ,
,即
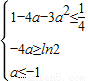 ,解得a
,解得a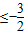 ,
,故a的取值范围为
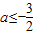 .
. (3)构造函数
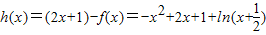 ,
,则
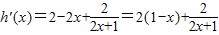 ,
,当x∈[0,1]时,h′(x)>0,∴函数h(x)在[0,1]上单调递增,
又h(0)=1-ln2>0,
∴x∈[0,1]时,恒有h(x)>h(0)>0,即
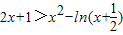 恒成立,
恒成立,故对任意正整数n,取
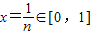 ,有
,有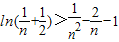 .
.点评:本题考查利用导数研究函数的单调性、函数的最值,考查转化思想,考查学生分析问题解决问题的能力,解决(3)问的关键是根据目标式恰当构造函数.

练习册系列答案
相关题目