题目内容
已知正方体的棱长为a(a>0),则它的内切球与外接球的表面积之比为( )
A、1:
| ||
| B、1:3 | ||
C、1:3
| ||
| D、1:9 |
分析:根据正方体的内切球与外接球的半径与正方体棱长之间的关系进行求解即可.
解答:解:设正方体的内切球与外接球半径分别为r,R.
则正方体的内切球的直径2r=a,则r=
,
则正方体的外接球的直径2R=
a,则R=
,
∴r:R=1:
,
∴内切球与外接球的表面积之比为r2:R2=1:3.
故选:B.
则正方体的内切球的直径2r=a,则r=
| a |
| 2 |
则正方体的外接球的直径2R=
| 3 |
| ||
| 2 |
∴r:R=1:
| 3 |
∴内切球与外接球的表面积之比为r2:R2=1:3.
故选:B.
点评:本题主要考查球的表面积公式以及正方体与球的相切和内接关系,要求熟练掌握球半径如正方体的边长关系.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目
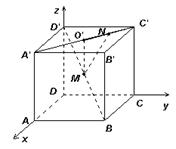
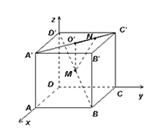
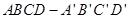 的棱长为a,M为
的棱长为a,M为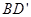 的中点,点N在
的中点,点N在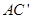 上,且
上,且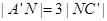 ,试求MN的长.
,试求MN的长.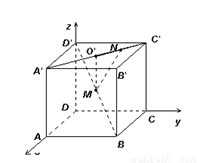
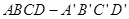 的棱长为a,M为
的棱长为a,M为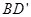 的中点,点N在
的中点,点N在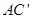 '上,且
'上,且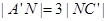 ,试求MN的长.
,试求MN的长.