题目内容
(本题满分16分)
已知![]() 两点的坐标分别为
两点的坐标分别为![]() 、
、![]() ,动点
,动点![]() 满足
满足![]() .
.
(1)求动点![]() 的轨迹方程;
的轨迹方程;
(2)若点![]() 在(1)中的轨迹上,且满足
在(1)中的轨迹上,且满足![]() 为直角三角形,求点
为直角三角形,求点![]() 的坐标;
的坐标;
(3)设经过![]() 点的直线
点的直线![]() 与(1)中的轨迹交于
与(1)中的轨迹交于![]() 两点,问是否存在这样的直线
两点,问是否存在这样的直线![]() 使得
使得![]() 为正三角形,若存在求出直线
为正三角形,若存在求出直线![]() 的方程,若不存在说明理由.
的方程,若不存在说明理由.
(本题满分16分)
解:(1)∵![]()
∴![]() 点的轨迹是以
点的轨迹是以![]() 为焦点,长轴为
为焦点,长轴为![]() 的椭圆:
的椭圆:![]() …5分
…5分
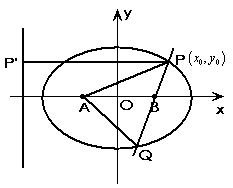
(2)如图:
①以![]() 为直角顶点时,点
为直角顶点时,点![]() 的坐标为:
的坐标为: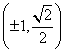
②以![]() 为直角顶点时,设点
为直角顶点时,设点![]() 的坐标为
的坐标为![]() ,根据直角三角形的性质知:
,根据直角三角形的性质知:
![]() ,即:
,即: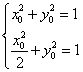 ,解之得:
,解之得:![]() 。………………11分
。………………11分
【或:由![]() 知:此时
知:此时![]() 为短轴端点
为短轴端点![]() 】
】
(3)因为![]() 为正三角形,所以
为正三角形,所以![]()
设点![]() 的坐标为
的坐标为![]() ,轴椭圆的第二定义知:
,轴椭圆的第二定义知:![]() ,即
,即![]()
 所以:
所以:![]() ,
,
所以![]() 的直线方程为:
的直线方程为:![]() ………16分
………16分

练习册系列答案
相关题目


 在
在 上的单调性;
上的单调性; ,使
,使 ,则称
,则称 的不动点,现已知该函数有且仅有一个不动点,求
的不动点,现已知该函数有且仅有一个不动点,求 的值;
的值; 在
在