题目内容
已知函数![]()
(Ⅰ)求函数的定义域,并证明![]() 在定义域上是奇函数;
在定义域上是奇函数;
(Ⅱ)若![]()
![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)当![]() 时,试比较
时,试比较![]() 与
与![]() 的大小关系.
的大小关系.
解:(Ⅰ)由![]() ,解得
,解得![]() 或
或![]() ,
,
∴ 函数的定义域为![]() ………2分
………2分
当![]() 时,
时,
![]()
∴ ![]() 在定义域上是奇函数。 ………4分
在定义域上是奇函数。 ………4分
(Ⅱ)由![]() 时,
时,![]() 恒成立,
恒成立,
∴![]()
∴ ![]() 在
在![]() 成立 ………6分
成立 ………6分
令![]() ,
,![]() ,由二次函数的性质可知
,由二次函数的性质可知
![]() 时函数单调递增,
时函数单调递增,![]() 时函数单调递减,
时函数单调递减,
![]() 时,
时,![]()
∴![]() ………8分
………8分
(Ⅲ)![]() =
=![]() …9分
…9分
证法一:构造函数![]() ,
,![]()
当![]() 时,
时,![]() ,∴
,∴![]() 在
在![]() 单调递减,
单调递减,
![]() ………12分
………12分
当![]() (
(![]() )时,
)时,![]()
![]() …14分
…14分
证法二:构造函数![]() ,证明:
,证明:![]() 在
在![]() 成立,则当
成立,则当![]() 时,
时,![]() 成立.
成立.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 的定义域;
的定义域; 为何值时,函数值大于1.
为何值时,函数值大于1.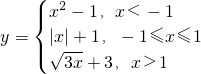 编写一程序求函数值.
编写一程序求函数值. 编写一程序求函数值.
编写一程序求函数值. 编写一程序求函数值.
编写一程序求函数值.