题目内容
已知f(x)=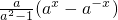 ,(a>0且a≠1)
,(a>0且a≠1)
(1)判断f(x)的奇偶性.
(2)讨论f(x)的单调性.
(3)当x∈[-1,1]时,f(x)≥b恒成立,求b的取值范围.
解:(1)∵f(x)=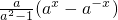 ,
,
所以f(x)定义域为R,
又f(-x)= (a-x-ax)=-
(a-x-ax)=- (ax-a-x)=-f(x),
(ax-a-x)=-f(x),
所以函数f(x)为奇函数,
(2)任取x1<x2
则f(x2)-f(x1)= (ax2-ax1)(1+a-(x1+x2))
(ax2-ax1)(1+a-(x1+x2))
∵x1<x2,且a>0且a≠1,1+a-(x1+x2)>0
①当a>1时,a2-1>0,ax2-ax1>0,则有f(x2)-f(x1)>0,
②当0<a<1时,a2-1<0.,ax2-ax1<0,则有f(x2)-f(x1)>0,
所以f(x)为增函数;
(3)当x∈[-1,1]时,f(x)≥b恒成立,
即b小于等于f(x)的最小值,
由(2)知当x=-1时,f(x)取得最小值,最小值为 (
(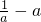 )=-
)=- ,
,
∴b≤- .
.
求b的取值范围(-∞,- ].
].
分析:(1)由函数的解析式可求函数的定义域,先证奇偶性:代入可得f(-x)=-f(x),从而可得函数为奇函数;
(2)再证单调性:利用定义任取x1<x2,利用作差比较f(x1)-f(x2)的正负,从而确当f(x1)与f(x2)的大小,进而判断函数的单调性;
(3)对一切x∈[-1,1]恒成立,转化为b小于等于f(x)的最小值,利用(2)的结论求其最小值,从而建立不等关系解之即可.
点评:本题考查了函数的奇偶性的判断,函数单调性的证明,抽象函数性质应用,关键是正确应用函数的基本性质解题.
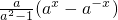 ,
,所以f(x)定义域为R,
又f(-x)=
 (a-x-ax)=-
(a-x-ax)=- (ax-a-x)=-f(x),
(ax-a-x)=-f(x),所以函数f(x)为奇函数,
(2)任取x1<x2
则f(x2)-f(x1)=
 (ax2-ax1)(1+a-(x1+x2))
(ax2-ax1)(1+a-(x1+x2))∵x1<x2,且a>0且a≠1,1+a-(x1+x2)>0
①当a>1时,a2-1>0,ax2-ax1>0,则有f(x2)-f(x1)>0,
②当0<a<1时,a2-1<0.,ax2-ax1<0,则有f(x2)-f(x1)>0,
所以f(x)为增函数;
(3)当x∈[-1,1]时,f(x)≥b恒成立,
即b小于等于f(x)的最小值,
由(2)知当x=-1时,f(x)取得最小值,最小值为
 (
(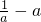 )=-
)=- ,
,∴b≤-
 .
.求b的取值范围(-∞,-
 ].
].分析:(1)由函数的解析式可求函数的定义域,先证奇偶性:代入可得f(-x)=-f(x),从而可得函数为奇函数;
(2)再证单调性:利用定义任取x1<x2,利用作差比较f(x1)-f(x2)的正负,从而确当f(x1)与f(x2)的大小,进而判断函数的单调性;
(3)对一切x∈[-1,1]恒成立,转化为b小于等于f(x)的最小值,利用(2)的结论求其最小值,从而建立不等关系解之即可.
点评:本题考查了函数的奇偶性的判断,函数单调性的证明,抽象函数性质应用,关键是正确应用函数的基本性质解题.

练习册系列答案
相关题目
已知f(x)=e3ax-3ax(a≠0),则
的值为( )
| lim |
| x→0 |
| f′(x) |
| eax-1 |
| A、a | B、2a | C、3a | D、9a |
已知f(x)=alnx+
x2(a>0),若对任意两个不等的正实数x1,x2,都有
>2恒成立,则a的取值范围是( )
| 1 |
| 2 |
| f(x1)-f(x2) |
| x1-x2 |
| A、(0,1] |
| B、(1,+∞) |
| C、(0,1) |
| D、[1,+∞) |