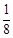题目内容
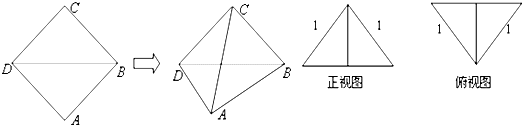
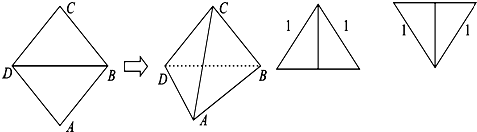
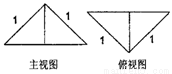
 把边长为1的正方形ABCD沿对角线BD折起,形成三 棱锥C-ABD,它的主视图与俯视图如图所示,则二面角 C-AB-D的正切值为
把边长为1的正方形ABCD沿对角线BD折起,形成三 棱锥C-ABD,它的主视图与俯视图如图所示,则二面角 C-AB-D的正切值为| 2 |
| 2 |
分析:由题意确定几何体的形状,二面角C-BD-A为直角二面角,进一步作出二面角 C-AB-D的平面角,即可求得二面角 C-AB-D的正切值.
解答: 解:根据这两个视图可以推知折起后二面角C-BD-A为直二面角,如图,取BD的中点O,AB的中点E,连接OE,CE,则
解:根据这两个视图可以推知折起后二面角C-BD-A为直二面角,如图,取BD的中点O,AB的中点E,连接OE,CE,则
∵CO⊥BD,∴CO⊥平面ABD
∵O是BD的中点,E是AB的中点
∴OE∥AD
∵AB⊥AD
∴OE⊥AB
∵CO⊥平面ABD
∴CE⊥AB
∴∠CEO为二面角 C-AB-D的平面角
∵CO=
,OE=
∴tan∠CEO=
=
故答案为:
 解:根据这两个视图可以推知折起后二面角C-BD-A为直二面角,如图,取BD的中点O,AB的中点E,连接OE,CE,则
解:根据这两个视图可以推知折起后二面角C-BD-A为直二面角,如图,取BD的中点O,AB的中点E,连接OE,CE,则∵CO⊥BD,∴CO⊥平面ABD
∵O是BD的中点,E是AB的中点
∴OE∥AD
∵AB⊥AD
∴OE⊥AB
∵CO⊥平面ABD
∴CE⊥AB
∴∠CEO为二面角 C-AB-D的平面角
∵CO=
| ||
| 2 |
| 1 |
| 2 |
∴tan∠CEO=
| CO |
| OE |
| 2 |
故答案为:
| 2 |
点评:本题考查三视图与直观图的互化,考查面面角,解题的关键是确定几何体的形状,属于中档题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
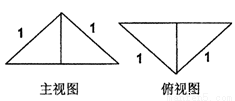
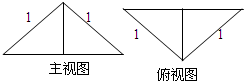 把边长为1的正方形ABCD沿对角线BD折起,形成的三棱锥C-ABD的主视图与俯视图如图所示,则左视图的面积为( )
把边长为1的正方形ABCD沿对角线BD折起,形成的三棱锥C-ABD的主视图与俯视图如图所示,则左视图的面积为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
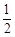 B.
B. C.
C.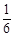 D.
D.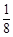
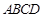 沿对角线
沿对角线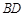 折起形成三棱锥
折起形成三棱锥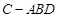 的主视图与俯视图如图所示,则左视图的面积为(
)
的主视图与俯视图如图所示,则左视图的面积为(
)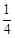 B.
B.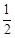
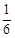 D.
D.