题目内容
(2012•虹口区三模)设
,
为二个非零向量,且|
+
|=2,|
-
|=2,则|
|+|
|的最大值是
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
2
| 2 |
2
.| 2 |
分析:根据向量数量积的性质和模的定义,将已知两个等式两边平方再相加,得2
2+2
2 =8,再利用基本不等式,即可求出|
|+|
|的最大值.
| |a| |
| |b| |
| a |
| b |
解答:解:∵|
+
|=2,|
-
|=2,
∴
+
2=
2+2
•
+
2 =4,…①
且
-
2=
2-2
•
+
2 =4,…②
①+②,得2
2+2
2 =8,
根据基本不等式,得(|
|+|
|)2≤2
2+2
2 =8,
∴当且仅当|
|=|
|=
时,|
|+|
|的最大值是
=2
故答案为:2
| a |
| b |
| a |
| b |
∴
| |a |
| b| |
| |a| |
| a |
| b |
| |b| |
且
| |a |
| b| |
| |a| |
| a |
| b |
| |b| |
①+②,得2
| |a| |
| |b| |
根据基本不等式,得(|
| a |
| b |
| |a| |
| |b| |
∴当且仅当|
| a |
| b |
| 2 |
| a |
| b |
| 8 |
| 2 |
故答案为:2
| 2 |
点评:本题给出两个非零向量的和与差的长度,求它们长度之和的最大值,着重考查了平面向量数量积的运算性质和基本不等式等知识点,属于基础题.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
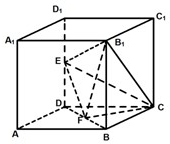 (2012•虹口区三模)如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.
(2012•虹口区三模)如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点. (2012•虹口区三模)函数y=2x和y=x3的图象的示意图如图所示,设两函数的图象交于点A(x1,y1),B(x2,y2),且x1<x2.
(2012•虹口区三模)函数y=2x和y=x3的图象的示意图如图所示,设两函数的图象交于点A(x1,y1),B(x2,y2),且x1<x2.