题目内容
2.已知等差数列{an}的前n项和为Sn,且a2=-5,a6-a4=6,求:(1)通项公式an;
(2)前10项和S10.
分析 (1)利用等差数列的通项公式即可得出;
(2)利用等差数列的前n项和公式即可得出.
解答 解:(1)设等差数列{an}的公差为d,∵a2=-5,a6-a4=6,
∴$\left\{\begin{array}{l}{{a}_{1}+d=-5}\\{2d=6}\end{array}\right.$,解得d=3,a1=-8.
∴an=-8+3(n-1)=3n-11.
(2)S10=10×(-8)+$\frac{10×9}{2}×3$=55.
点评 本题考查了等差数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.一个几何体的三视图如图所示,则这个几何体的侧面积为( )


| A. | $\frac{\sqrt{3}}{3}$π | B. | 2π | C. | 3π | D. | 4π |
9.方程x(x2+y2-4)=0与x2+(x2+y2-4)2=0表示的曲线是( )
| A. | 都表示一条直线和一个圆 | |
| B. | 都表示两个点 | |
| C. | 前者是两个点,后者是一直线和一个圆 | |
| D. | 前者是一条直线和一个圆,后者是两个点 |
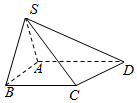 如图:在四棱锥S-ABCD中,已知∠DAB=∠ABC=90°,SA⊥平面ABCD,SA=AB=BC=a,AD=2a,求直线SD与AC所成的角的大小.
如图:在四棱锥S-ABCD中,已知∠DAB=∠ABC=90°,SA⊥平面ABCD,SA=AB=BC=a,AD=2a,求直线SD与AC所成的角的大小. 已知函数f(x)=Asin(ωx+φ)(A>0,w>0,|φ|<$\frac{π}{2}$)在一个周期内的图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,w>0,|φ|<$\frac{π}{2}$)在一个周期内的图象如图所示.