题目内容
19．已知点A（0，2），抛物线C1：y2=ax（a＞0）的焦点为F，射线FA与抛物线C相交于点M，与其准线相交于点N，若|FM|：|MN|=1：$\sqrt{5}$，则a的值等于4．分析 作出M在准线上的射影，根据|KM|：|MN|确定|KN|：|KM|的值，进而列方程求得a．
解答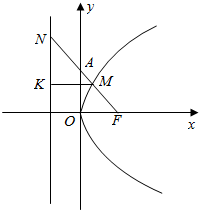 
解：依题意F点的坐标为（$\frac{a}{4}$，0），
设M在准线上的射影为K，
由抛物线的定义知|MF|=|MK|，
∴|KM|：|MN|=1：$\sqrt{5}$，
则|KN|：|KM|=2：1，
kFN=$\frac{0-2}{\frac{a}{4}-0}$=-$\frac{2}{\frac{a}{4}}$，
kFN=-$\frac{|KN|}{|KM|}$=-2
∴$\frac{2}{\frac{a}{4}}$=2，求得a=4，
故答案为：4．
点评 本题主要考查了抛物线的简单性质．抛物线中涉及焦半径的问题常利用抛物线的定义转化为点到准线的距离来解决．
练习册系列答案
相关题目
6．某市为了了解市民对本市文明建设的满意程度，通过问卷调查了学生、在职人员、退休人员共250人，结果如表：
若在职人员中随机抽取1人，恰好抽到学生的概率为0.32．
（1）求x的值；
（2）若y≥70，z≥2，求市民对市政管理满意度不小于0.9的概率．
（注：满意度=$\frac{满意人数}{总人数}$）
| 学生 | 在职人员 | 退休人员 | |
| 满意 | x | y | 78 |
| 不满意 | 5 | z | 12 |
（1）求x的值；
（2）若y≥70，z≥2，求市民对市政管理满意度不小于0.9的概率．
（注：满意度=$\frac{满意人数}{总人数}$）
10．已知△ABC的三边AB=$\sqrt{{a}^{2}+{b}^{2}}$，BC=$\sqrt{{b}^{2}+{c}^{2}}$，CA=$\sqrt{{c}^{2}+{a}^{2}}$ 其中a，b，c＞0，则△ABC的形状是 （ ）
| A． | 锐角三角形 | B． | 直角三角形 | C． | 钝角三角形 | D． | 以上答案都不对 |