题目内容
已知 的周长为
的周长为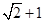 ,且
,且
(1)求边 的长;
的长;
(2)若 的面积为
的面积为 ,求角
,求角 .
.
(1)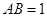 ;(2)
;(2)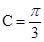
解析试题分析:(1)由题中所给三角形周长,即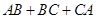 为已知,又由
为已知,又由 结合正弦定理可化角为边得到关于边的关系式
结合正弦定理可化角为边得到关于边的关系式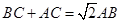 ,由上述所得这两式,就可求得
,由上述所得这两式,就可求得 的值; (2)由三角形的面积公式
的值; (2)由三角形的面积公式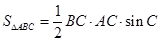 ,结合已知
,结合已知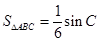 可以求得
可以求得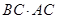 的值,结合余弦定理得
的值,结合余弦定理得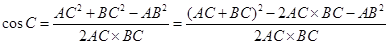 ,这样即可求出
,这样即可求出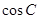 的值,又结合三角形中
的值,又结合三角形中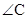 的范围,进而得到
的范围,进而得到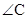 的值.
的值.
试题解析:解:(1)由题意及正弦定理得: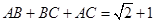 ,
,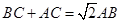 ,
,
两式相减得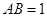 . (6分)
. (6分)
(2)由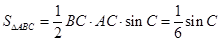 ,得
,得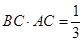 , (8分)
, (8分)
由余弦定理得,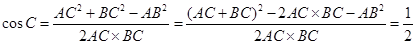 ,又
,又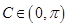 ,
,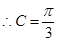 (14分)
(14分)
考点:1.正弦定理;2.余弦定理;3.三角形面积公式

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
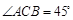 ,求天宁宝塔AB与大楼CD底部之间的距离BD.
,求天宁宝塔AB与大楼CD底部之间的距离BD.
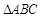 中,已知
中,已知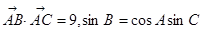 ,又
,又 的面积等于6.
的面积等于6.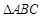 的三边之长;
的三边之长;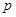 是
是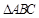 (含边界)内一点,
(含边界)内一点,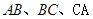 的距离分别为
的距离分别为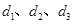 ,求
,求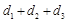 的取值范围.
的取值范围.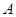 、
、 、
、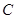 三个工作点,需要建立一个公共无线网络发射点
三个工作点,需要建立一个公共无线网络发射点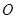 ,使得发射点到三个工作点的距离相等.已知这三个工作点之间的距离分别为
,使得发射点到三个工作点的距离相等.已知这三个工作点之间的距离分别为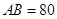
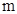 ,
,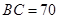
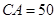
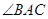 的大小;
的大小;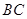 的距
的距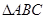 中,设内角
中,设内角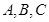 的对边分别为
的对边分别为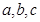 ,向量
,向量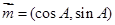 ,向量
,向量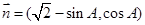 ,若
,若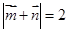
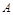 的大小;
的大小;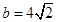 ,且
,且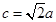 ,求
,求 ,
, ,其中ω>0,函数
,其中ω>0,函数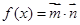 ,若
,若 相邻两对称轴间的距离为
相邻两对称轴间的距离为 .
. ,△ABC的面积S=5
,△ABC的面积S=5 ,b=4,,求a.
,b=4,,求a. 中,
中,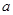 、
、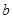 、
、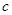 是三个内角
是三个内角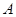 、
、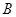 、
、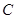 的对边,关于
的对边,关于 的不等式
的不等式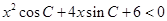 的解集是空集.
的解集是空集.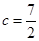 ,
,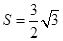 ,求当角
,求当角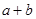 的值.
的值. 中,角
中,角 的对边分别为
的对边分别为 ,且
,且 .
. 的值;
的值; ,且
,且 ,求
,求 和
和 的值.
的值. 是
是 的内角,
的内角, 分别是其对边长,且
分别是其对边长,且 .
. ,求
,求 的长;
的长; 的对边
的对边 ,求
,求