题目内容
已知△ABC中,B(1,0)、C(5,0),点A在x轴上方移动,且tanB+tanC=3,则△ABC的重心G的轨迹方程为________.
y-1=- (x-3)2(x≠
(x-3)2(x≠ 且x≠
且x≠ )
)
分析:设A(x0,y0),由tanB+tanC=3可求得x0和y0之间的关系式,设G(x,y)为△ABC的重心,
则由重心坐标公式:x=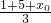 ,y=
,y=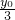 ,解出x0和y0,代入x0和y0的关系式,即得G的轨迹方程,所用方法为相关点代入法.
,解出x0和y0,代入x0和y0的关系式,即得G的轨迹方程,所用方法为相关点代入法.
解答:设A(x0,y0),∵tanB+tanC=3,
∴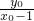 -
-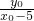 =3,点A的轨迹方程为y0=-
=3,点A的轨迹方程为y0=- (x02-6x0+5)(x0≠1且x0≠5).
(x02-6x0+5)(x0≠1且x0≠5).
若G(x,y)为△ABC的重心,则由重心坐标公式:x=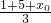 ,y=
,y=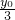 ,∴x0=3x-6,且y0=3y.
,∴x0=3x-6,且y0=3y.
代入A点轨迹方程得G的轨迹方程为y-1=- (x-3)2(x≠
(x-3)2(x≠ 且x≠
且x≠ ).
).
故答案为:y-1=- (x-3)2(x≠
(x-3)2(x≠ 且x≠
且x≠ )
)
点评:本题考查求轨迹方程的方法:相关点代入法.在用此法时,注意求哪个点的轨迹方程,就设此点坐标为(x,y).
 (x-3)2(x≠
(x-3)2(x≠ 且x≠
且x≠ )
)分析:设A(x0,y0),由tanB+tanC=3可求得x0和y0之间的关系式,设G(x,y)为△ABC的重心,
则由重心坐标公式:x=
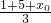 ,y=
,y=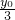 ,解出x0和y0,代入x0和y0的关系式,即得G的轨迹方程,所用方法为相关点代入法.
,解出x0和y0,代入x0和y0的关系式,即得G的轨迹方程,所用方法为相关点代入法.解答:设A(x0,y0),∵tanB+tanC=3,
∴
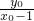 -
-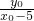 =3,点A的轨迹方程为y0=-
=3,点A的轨迹方程为y0=- (x02-6x0+5)(x0≠1且x0≠5).
(x02-6x0+5)(x0≠1且x0≠5).若G(x,y)为△ABC的重心,则由重心坐标公式:x=
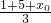 ,y=
,y=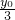 ,∴x0=3x-6,且y0=3y.
,∴x0=3x-6,且y0=3y.代入A点轨迹方程得G的轨迹方程为y-1=-
 (x-3)2(x≠
(x-3)2(x≠ 且x≠
且x≠ ).
).故答案为:y-1=-
 (x-3)2(x≠
(x-3)2(x≠ 且x≠
且x≠ )
)点评:本题考查求轨迹方程的方法:相关点代入法.在用此法时,注意求哪个点的轨迹方程,就设此点坐标为(x,y).

练习册系列答案
相关题目