题目内容
已知一个球内切于圆锥.求证:它们的全面积之比等于它们的体积之比.
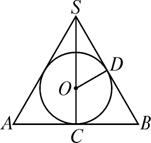
证明:设圆锥的底面半径、高和母线长分别为r、h、l,内切球的半径为R,如图所示的圆锥的轴截面图中,D为母线SB与球的切点,O为球心,连结OD,则OD⊥SB.由Rt△SOD∽Rt△SBC,知![]() ,
,
即![]() .解得
.解得![]() .
.
所以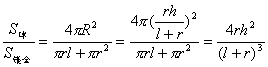 ,
,
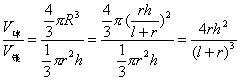 .
.
所以S球∶S锥全=V球∶V锥.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
题目内容
已知一个球内切于圆锥.求证:它们的全面积之比等于它们的体积之比.
证明:设圆锥的底面半径、高和母线长分别为r、h、l,内切球的半径为R,如图所示的圆锥的轴截面图中,D为母线SB与球的切点,O为球心,连结OD,则OD⊥SB.由Rt△SOD∽Rt△SBC,知![]() ,
,
即![]() .解得
.解得![]() .
.

所以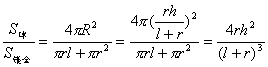 ,
,
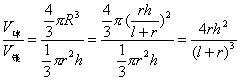 .
.
所以S球∶S锥全=V球∶V锥.

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案