题目内容
(理科加试题)若二项式(| 2 | |||
|
| x |
(1)求n的值;
(2)求展开式中系数最大的项.
分析:(1)利用二项展开式的通项公式求出展开式的通项,令x的指数为0,据题意当r=4时x的指数为0,代入求出n的值.
(2)将n的值代入通项,求出通项的系数,设第k+1项的系数最大,令其大于等于前一项的系数同时大于等于后一项的系数,利用组合数公式解不等式求出k的值,代入通项即可.
(2)将n的值代入通项,求出通项的系数,设第k+1项的系数最大,令其大于等于前一项的系数同时大于等于后一项的系数,利用组合数公式解不等式求出k的值,代入通项即可.
解答:解:(1)∵Tr+1=
(
)n-r(
)r,
x的指数为-
+
=0,
∵(
+
)n的展开式中的常数项为第五项,
∴r=4,
解得:n=10.
(2)∵Tr+1=
(
)10-r(
)r,
其系数为C10r•210-r.
设第k+1项的系数最大,则
化简得:
即
≤k≤
,
∴k=3,
即第四项系数最大,T4=
•27•x-
=15360x-
.
| C | r n |
| 2 | |||
|
| x |
x的指数为-
| n-r |
| 3 |
| r |
| 2 |
∵(
| 2 | |||
|
| x |
∴r=4,
解得:n=10.
(2)∵Tr+1=
| C | r 10 |
| 2 | |||
|
| x |
其系数为C10r•210-r.
设第k+1项的系数最大,则
|
化简得:
|
| 8 |
| 3 |
| 11 |
| 3 |
∴k=3,
即第四项系数最大,T4=
| C | 3 10 |
| 5 |
| 6 |
| 5 |
| 6 |
点评:解决二项展开式的特定项问题常利用的工具是二项展开式的通项公式;求二项展开式的项的最大系数问题,常令其大于等于前一项的系数同时大于等于后一项的系数,解不等式即可.

练习册系列答案
相关题目
 的展开式中的常数项为第五项.
的展开式中的常数项为第五项.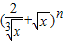 的展开式中的常数项为第五项.
的展开式中的常数项为第五项.