题目内容
已知函数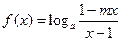
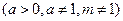 是奇函数.
是奇函数.
(1)求实数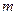 的值;
的值;
(2)判断函数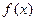 在
在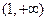 上的单调性,并给出证明;
上的单调性,并给出证明;
(3)当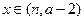 时,函数
时,函数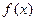 的值域是
的值域是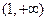 ,求实数
,求实数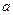 与
与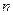 的值
的值
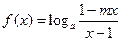
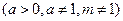 是奇函数.
是奇函数.(1)求实数
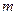 的值;
的值;(2)判断函数
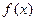 在
在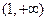 上的单调性,并给出证明;
上的单调性,并给出证明;(3)当
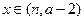 时,函数
时,函数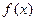 的值域是
的值域是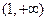 ,求实数
,求实数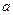 与
与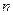 的值
的值1解:(1)由已知条件得
 对定义域中的
对定义域中的 均成立.………………………………1分
均成立.………………………………1分

即


 对定义域中的
对定义域中的 均成立.
均成立.

即
 (舍去)或
(舍去)或 . …………………………………4分
. …………………………………4分(2)由(1)得

设
 ,
, 当
当 时,
时,

 . ………………………………6分
. ………………………………6分当
 时,
时, ,即
,即 .
. 当
当 时,
时,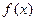 在
在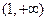 上是减函数. …
上是减函数. … …………
………… …………………8分
…………………8分同理当
 时,
时,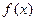 在
在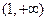 上是增函数. ………………………10分
上是增函数. ………………………10分(3)
 函数
函数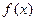 的定义域为
的定义域为 ,
, ①
① ,
,
 .
.
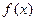 在
在 为增函数,
为增函数,要使值域为
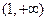 ,
,则
 (无解)
(无解) ②
 ,
, 
 .
.
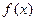 在
在 为减函数,
为减函数,要使
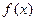 的值域为
的值域为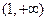 , 则
, 则

 ,
, . ……………………………14分
. ……………………………14分略

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
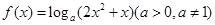 在区间
在区间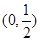 内恒有
内恒有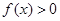 ,则
,则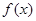 的单调递增区间为( )
的单调递增区间为( )




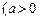 且
且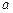 ≠1)
≠1)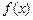 的单调性。(12分)
的单调性。(12分)
 (
( )=
)= ,
,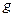 (
( 且
且 .
. =4,
=4, ),且F(
),且F( 的值;
的值;
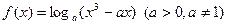 在区间
在区间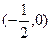 内单调递增,则a的
内单调递增,则a的



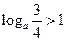 ,则实数a的取值范围是
,则实数a的取值范围是




 的定义域是
的定义域是  .
. 若
若 ,则
,则 ( )
( )  或
或
