ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΓΨ2017±±Ψ©Ές≥««χ5‘¬ΡΘΡβΓΩΡ≥¥σ―ßΈΣΒς―–―ß…ζ‘Ύ![]() Θ§
Θ§![]() ΝΫΦ“≤ΆΧϋ”Ο≤ΆΒΡ¬ζ“βΕ»Θ§¥”‘Ύ
ΝΫΦ“≤ΆΧϋ”Ο≤ΆΒΡ¬ζ“βΕ»Θ§¥”‘Ύ![]() Θ§
Θ§![]() ΝΫΦ“≤ΆΧϋΕΦ”ΟΙΐ≤ΆΒΡ―ß…ζ÷–ΥφΜζ≥ι»ΓΝΥ100»ΥΘ§ΟΩ»ΥΖ÷±πΕ‘’βΝΫΦ“≤ΆΧϋΫχ––ΤάΖ÷Θ§¬ζΖ÷ΨυΈΣ60Ζ÷.
ΝΫΦ“≤ΆΧϋΕΦ”ΟΙΐ≤ΆΒΡ―ß…ζ÷–ΥφΜζ≥ι»ΓΝΥ100»ΥΘ§ΟΩ»ΥΖ÷±πΕ‘’βΝΫΦ“≤ΆΧϋΫχ––ΤάΖ÷Θ§¬ζΖ÷ΨυΈΣ60Ζ÷.
’ϊάμΤάΖ÷ ΐΨίΘ§ΫΪΖ÷ ΐ“‘10ΈΣΉιΨύΖ÷≥…6ΉιΘΚ![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§ΒΟΒΫ
Θ§ΒΟΒΫ![]() ≤ΆΧϋΖ÷ ΐΒΡΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΘ§ΚΆ
≤ΆΧϋΖ÷ ΐΒΡΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΘ§ΚΆ![]() ≤ΆΧϋΖ÷ ΐΒΡΤΒ ΐΖ÷≤Φ±μΘΚ
≤ΆΧϋΖ÷ ΐΒΡΤΒ ΐΖ÷≤Φ±μΘΚ
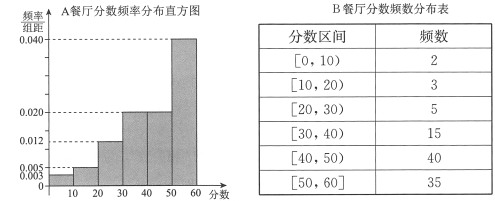
Ε®“ε―ß…ζΕ‘≤ΆΧϋΤάΦέΒΡΓΑ¬ζ“βΕ»÷Η ΐΓ±»γœ¬ΘΚ
Ζ÷ ΐ |
|
|
|
¬ζ“βΕ»÷Η ΐ |
|
|
|
Θ®ΔώΘ©‘Ύ≥ι―υΒΡ100»Υ÷–Θ§«σΕ‘![]() ≤ΆΧϋΤάΦέΓΑ¬ζ“βΕ»÷Η ΐΓ±ΈΣ0ΒΡ»Υ ΐΘΜ
≤ΆΧϋΤάΦέΓΑ¬ζ“βΕ»÷Η ΐΓ±ΈΣ0ΒΡ»Υ ΐΘΜ
Θ®ΔρΘ©¥”ΗΟ–Θ‘Ύ![]() Θ§
Θ§![]() ΝΫΦ“≤ΆΧϋΕΦ”ΟΙΐ≤ΆΒΡ―ß…ζ÷–ΥφΜζ≥ι»Γ1»ΥΫχ––Βς≤ιΘ§ ‘ΙάΦΤΤδΕ‘
ΝΫΦ“≤ΆΧϋΕΦ”ΟΙΐ≤ΆΒΡ―ß…ζ÷–ΥφΜζ≥ι»Γ1»ΥΫχ––Βς≤ιΘ§ ‘ΙάΦΤΤδΕ‘![]() ≤ΆΧϋΤάΦέΒΡΓΑ¬ζ“βΕ»÷Η ΐΓ±±»Ε‘
≤ΆΧϋΤάΦέΒΡΓΑ¬ζ“βΕ»÷Η ΐΓ±±»Ε‘![]() ≤ΆΧϋΤάΦέΒΡΓΑ¬ζ“βΕ»÷Η ΐΓ±ΗΏΒΡΗ≈¬ ΘΜ
≤ΆΧϋΤάΦέΒΡΓΑ¬ζ“βΕ»÷Η ΐΓ±ΗΏΒΡΗ≈¬ ΘΜ
Θ®ΔσΘ©»γΙϊ¥”![]() Θ§
Θ§![]() ΝΫΦ“≤ΆΧϋ÷–―Γ‘ώ“ΜΦ“”Ο≤ΆΘ§ΡψΜα―Γ‘ώΡΡ“ΜΦ“ΘΩΥΒΟςάμ”….
ΝΫΦ“≤ΆΧϋ÷–―Γ‘ώ“ΜΦ“”Ο≤ΆΘ§ΡψΜα―Γ‘ώΡΡ“ΜΦ“ΘΩΥΒΟςάμ”….
ΓΨ¥πΑΗΓΩΘ®IΘ©![]() »ΥΘΜΘ®IIΘ©
»ΥΘΜΘ®IIΘ©![]() ΘΜΘ®IIIΘ©œξΦϊΫβΈω.
ΘΜΘ®IIIΘ©œξΦϊΫβΈω.
ΓΨΫβΈωΓΩ
Θ®ΔώΘ©”…Ε‘![]() ≤ΆΧϋΤάΖ÷ΒΡΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΘ§ΒΟ
≤ΆΧϋΤάΖ÷ΒΡΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΘ§ΒΟ
Ε‘![]() ≤ΆΧϋΓΑ¬ζ“βΕ»÷Η ΐΓ±ΈΣ0ΒΡΤΒ¬ ΈΣ
≤ΆΧϋΓΑ¬ζ“βΕ»÷Η ΐΓ±ΈΣ0ΒΡΤΒ¬ ΈΣ![]() Θ§
Θ§
Υυ“‘Θ§Ε‘![]() ≤ΆΧϋΤάΦέΓΑ¬ζ“βΕ»÷Η ΐΓ±ΈΣ0ΒΡ»Υ ΐΈΣ
≤ΆΧϋΤάΦέΓΑ¬ζ“βΕ»÷Η ΐΓ±ΈΣ0ΒΡ»Υ ΐΈΣ![]() .
.
Θ®ΔρΘ©…ηΓΑΕ‘![]() ≤ΆΧϋΤάΦέΓ°¬ζ“βΕ»÷Η ΐΓ·±»Ε‘
≤ΆΧϋΤάΦέΓ°¬ζ“βΕ»÷Η ΐΓ·±»Ε‘![]() ≤ΆΧϋΤάΦέΓ°¬ζ“βΕ»÷Η ΐΓ·ΗΏΓ±ΈΣ ¬Φΰ
≤ΆΧϋΤάΦέΓ°¬ζ“βΕ»÷Η ΐΓ·ΗΏΓ±ΈΣ ¬Φΰ![]() .
.
Φ«ΓΑΕ‘![]() ≤ΆΧϋΤάΦέΓ°¬ζ“βΕ»÷Η ΐΓ·ΈΣ1Γ±ΈΣ ¬Φΰ
≤ΆΧϋΤάΦέΓ°¬ζ“βΕ»÷Η ΐΓ·ΈΣ1Γ±ΈΣ ¬Φΰ![]() ΘΜΓΑΕ‘
ΘΜΓΑΕ‘![]() ≤ΆΧϋΤάΦέΓ°¬ζ“βΕ»÷Η ΐΓ·ΈΣ2Γ±ΈΣ ¬Φΰ
≤ΆΧϋΤάΦέΓ°¬ζ“βΕ»÷Η ΐΓ·ΈΣ2Γ±ΈΣ ¬Φΰ![]() ΘΜΓΑΕ‘
ΘΜΓΑΕ‘![]() ≤ΆΧϋΤάΦέΓ°¬ζ“βΕ»÷Η ΐΓ·ΈΣ0Γ±ΈΣ ¬Φΰ
≤ΆΧϋΤάΦέΓ°¬ζ“βΕ»÷Η ΐΓ·ΈΣ0Γ±ΈΣ ¬Φΰ![]() ΘΜΓΑΕ‘
ΘΜΓΑΕ‘![]() ≤ΆΧϋΤάΦέΓ°¬ζ“βΕ»÷Η ΐΓ·ΈΣ1Γ±ΈΣ ¬Φΰ
≤ΆΧϋΤάΦέΓ°¬ζ“βΕ»÷Η ΐΓ·ΈΣ1Γ±ΈΣ ¬Φΰ![]() .
.
Υυ“‘![]() Θ§
Θ§![]() Θ§
Θ§
”…”ΟΤΒ¬ ΙάΦΤΗ≈¬ ΒΟΘΚ![]() Θ§
Θ§![]() .
.
“ρΈΣ ¬Φΰ![]() ”κ
”κ![]() œύΜΞΕάΝΔΘ§Τδ÷–
œύΜΞΕάΝΔΘ§Τδ÷–![]() Θ§
Θ§![]() .
.
Υυ“‘![]()
![]()
![]()
Υυ“‘ΗΟ―ß…ζΕ‘![]() ≤ΆΧϋΤάΦέΒΡΓΑ¬ζ“βΕ»÷Η ΐΓ±±»Ε‘
≤ΆΧϋΤάΦέΒΡΓΑ¬ζ“βΕ»÷Η ΐΓ±±»Ε‘![]() ≤ΆΧϋΤάΦέΒΡΓΑ¬ζ“βΕ»÷Η ΐΓ±ΗΏΒΡΗ≈¬ ΈΣ
≤ΆΧϋΤάΦέΒΡΓΑ¬ζ“βΕ»÷Η ΐΓ±ΗΏΒΡΗ≈¬ ΈΣ![]() .
.
Θ®ΔσΘ©»γΙϊ¥”―ß…ζΕ‘![]() Θ§
Θ§![]() ΝΫΦ“≤ΆΧϋΤάΦέΒΡΓΑ¬ζ“βΕ»÷Η ΐΓ±ΒΡΤΎΆϊΫ«Ε»Ω¥ΘΚ
ΝΫΦ“≤ΆΧϋΤάΦέΒΡΓΑ¬ζ“βΕ»÷Η ΐΓ±ΒΡΤΎΆϊΫ«Ε»Ω¥ΘΚ
![]() ≤ΆΧϋΓΑ¬ζ“βΕ»÷Η ΐΓ±
≤ΆΧϋΓΑ¬ζ“βΕ»÷Η ΐΓ±![]() ΒΡΖ÷≤ΦΝ–ΈΣΘΚ
ΒΡΖ÷≤ΦΝ–ΈΣΘΚ
|
|
|
|
|
|
|
|
![]() ≤ΆΧϋΓΑ¬ζ“βΕ»÷Η ΐΓ±
≤ΆΧϋΓΑ¬ζ“βΕ»÷Η ΐΓ±![]() ΒΡΖ÷≤ΦΝ–ΈΣΘΚ
ΒΡΖ÷≤ΦΝ–ΈΣΘΚ
|
|
|
|
|
|
|
|
“ρΈΣ![]() ΘΜ
ΘΜ
![]() Θ§
Θ§
Υυ“‘![]() Θ§Μα―Γ‘ώ
Θ§Μα―Γ‘ώ![]() ≤ΆΧϋ”Ο≤Ά.
≤ΆΧϋ”Ο≤Ά.
ΉΔΘΚ±ΨΧβ¥πΑΗ≤ΜΈ®“Μ.÷Μ“ΣΩΦ…ζ―‘÷°ΚœάμΦ¥Ω….

ΓΨΧβΡΩΓΩΡ≥…ζ≤ζΦΉΘ§““ΝΫ÷÷≤ζΤΖΘ§…ζ≤ζ’βΝΫ÷÷≤ζΤΖΟΩΕ÷–η“ΣΒΡΟΚΘ§Βγ“‘ΦΑΟΩΕ÷≤ζΤΖΒΡ≤ζ÷Β»γ±μΥυ ΨΘ°»τΟΩΧλ≈δΗχΗΟ≥ßΒΡΟΚ÷ΝΕύ56Ε÷Θ§Ι©Βγ÷ΝΕύ45«ßΆΏΘ§Έ ΗΟ≥ß»γΚΈΑ≤≈≈…ζ≤ζΘ§ ΙΗΟ≥ß»’≤ζ÷ΒΉν¥σΘΩ
”ΟΟΚ/Ε÷ | ”ΟΒγ/«ßΆΏ | ≤ζ÷Β/Άρ‘Σ | |
ΦΉ÷÷≤ζΤΖ | 7 | 2 | 8 |
““÷÷≤ζΤΖ | 3 | 5 | 11 |
