Question

设地球的半径为R，在球坐标系中，点A的坐标为(R,45°,70°)，点B的坐标为(R,45°,160°)，求A、B两点的球面距离.

Answer 1

思路分析：要求A、B两点间球面距离，要把它放到△AOB中去分析，只要求得∠AOB的度数和AB的长度，就可求球面距离.

解：如图1-4-7，OB=R，由点A、B的球坐标可知∠BOO′=45°，∠AOO′=45°，这两个点都在北纬90°-45°=45°圈上，设纬度圈的圆心为O′，地球中心为O，则∠xOQ=70°，∠xOH=160°,

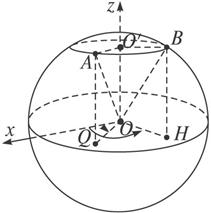
图1-4-7

∴∠AO′B=160°-70°=90°.

∵OB=R,O′B=O′A=R,

∴AB=R.连结AO、AB,则AO=BO=AB=R.

∴∠AOB=60°,

B=·2πR=R.

答:A、B两点间的球面距离为R.

    深化升华 要先将球坐标中的三度所表示的量在图形中找到.