题目内容
(本小题满分12分)已知抛物线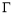 的顶点为坐标原点,焦点为
的顶点为坐标原点,焦点为 .
.
(Ⅰ)求抛物线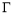 的方程;
的方程;
(Ⅱ)若点 为抛物线
为抛物线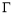 的准线上的任意一点,过点
的准线上的任意一点,过点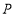 作抛物线
作抛物线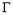 的切线
的切线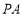 与
与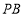 ,切点分别为
,切点分别为 ,求证:直线
,求证:直线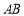 恒过某一定点;
恒过某一定点;
(Ⅲ)分析(Ⅱ)的条件和结论,反思其解题过程,再对命题(Ⅱ)进行变式和推广.请写出一个你发现的真命题,不要求证明(说明:本小题将根据所给出的命题的正确性和一般性酌情给分).
(Ⅰ)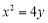 ; (Ⅱ)直线
; (Ⅱ)直线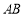 恒过定点
恒过定点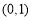 ; (Ⅲ)详见解析.
; (Ⅲ)详见解析.
【解析】
试题分析:(Ⅰ)依题意可设抛物线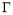 的方程为:
的方程为: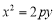 (
( ).由焦点为
).由焦点为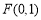 可知
可知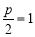 ,所以
,所以 .即可求出抛物线的方程.(Ⅱ)方法一:设切点
.即可求出抛物线的方程.(Ⅱ)方法一:设切点 、
、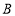 坐标分别为
坐标分别为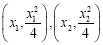 ,由(Ⅰ)知,
,由(Ⅰ)知,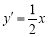 .
.
则切线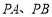 的斜率分别为
的斜率分别为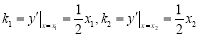 ,故切线
,故切线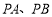 的方程分别为
的方程分别为 ,
,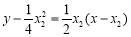 , 联立以上两个方程,得
, 联立以上两个方程,得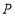 的坐标为
的坐标为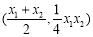 ,
,
因为点 在抛物线
在抛物线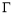 的准线上,所以
的准线上,所以 ,即
,即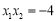 .设直线
.设直线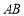 的方程为
的方程为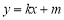 ,代入抛物线方程
,代入抛物线方程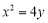 ,可得直线
,可得直线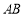 恒过定点
恒过定点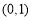 . 方法二:设切点
. 方法二:设切点 、
、 坐标分别为
坐标分别为 ,设
,设 ,
,
易知直线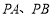 斜率必存在,可设过点
斜率必存在,可设过点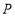 的切线方程为
的切线方程为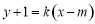 .
.
由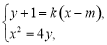 ,消去
,消去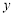 并整理得
并整理得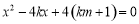 因为切线与抛物线有且只有一个交点,所以
因为切线与抛物线有且只有一个交点,所以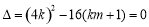 , 可得
, 可得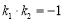 , 假设存在一定点,使得直线
, 假设存在一定点,使得直线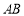 恒过该定点,则由抛物线对称性可知该定点必在
恒过该定点,则由抛物线对称性可知该定点必在 轴上,设该定点为
轴上,设该定点为 , 则
, 则 .又
.又 ,可得
,可得 ,所以直线
,所以直线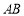 过定点
过定点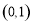 . (Ⅲ)根据直线与抛物线的位置关系的性质即可得到结论.
. (Ⅲ)根据直线与抛物线的位置关系的性质即可得到结论.
试题解析:【解析】
(Ⅰ)依题意可设抛物线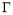 的方程为:
的方程为: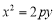 (
( ). 1分
). 1分
由焦点为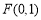 可知
可知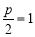 ,所以
,所以 . 2分
. 2分
所以所求的抛物线方程为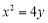 . 3分
. 3分
(Ⅱ)方法一:
设切点 、
、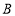 坐标分别为
坐标分别为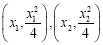 ,由(Ⅰ)知,
,由(Ⅰ)知,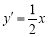 .
.
则切线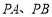 的斜率分别为
的斜率分别为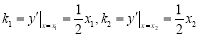 ,
,
故切线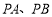 的方程分别为
的方程分别为 ,
,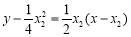 , 4分
, 4分
联立以上两个方程,得 .故
.故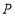 的坐标为
的坐标为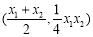 , 5分
, 5分
因为点 在抛物线
在抛物线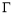 的准线上,所以
的准线上,所以 ,即
,即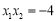 . 6分
. 6分
设直线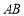 的方程为
的方程为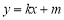 ,代入抛物线方程
,代入抛物线方程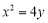 ,得
,得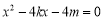 ,
,
所以 ,即
,即 ,所以
,所以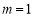 . 7分
. 7分
故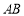 的方程为
的方程为 ,故直线
,故直线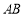 恒过定点
恒过定点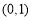 . 8分
. 8分
方法二:设切点 、
、 坐标分别为
坐标分别为 ,设
,设 ,
,
易知直线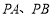 斜率必存在,可设过点
斜率必存在,可设过点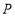 的切线方程为
的切线方程为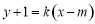 .
.
由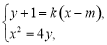 ,消去
,消去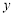 并整理得
并整理得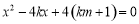 . ①
. ①
因为切线与抛物线有且只有一个交点,
所以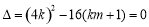 ,整理得
,整理得 , ②
, ②
所以直线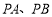 斜率
斜率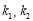 为方程②的两个根,故
为方程②的两个根,故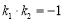 , 4分
, 4分
另一方面,由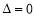 可得方程①的解为
可得方程①的解为 ,
,
所以 . 5分
. 5分
假设存在一定点,使得直线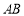 恒过该定点,则由抛物线对称性可知该定点必在
恒过该定点,则由抛物线对称性可知该定点必在 轴
轴
上,设该定点为 , 6分
, 6分
则 .
.
所以 ,
,
所以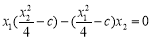 ,整理得
,整理得
所以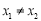 ,
,
所以 7分
7分
所以直线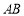 过定点
过定点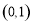 . 8分
. 8分
(Ⅲ)结论一:若点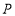 为直线
为直线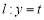 (
(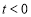 )上的任意一点,过点
)上的任意一点,过点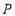 作抛物线
作抛物线
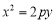 (
( )的切线
)的切线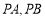 ,切点分别为
,切点分别为 ,则直线
,则直线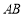 恒过定点
恒过定点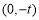 . 12分
. 12分
结论二:过点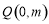 (
(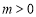 )任作一条直线交抛物线
)任作一条直线交抛物线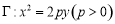 于
于 两点,分别以点
两点,分别以点 为切点作该抛物线的切线,两切线交于点
为切点作该抛物线的切线,两切线交于点 ,则点
,则点 必在定直线
必在定直线 上. 12分
上. 12分
结论三:已知点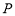 为直线
为直线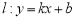 上的一点,若过点
上的一点,若过点 可以作两条直线与抛物线
可以作两条直线与抛物线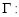
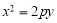 (
( )相切,切点分别为
)相切,切点分别为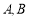 ,则直线
,则直线 恒过定点
恒过定点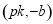 . 12分.
. 12分.
考点:1.抛物线方程;2.直线与抛物线的位置关系.

 阅读快车系列答案
阅读快车系列答案 的平均数是5,标准差是
的平均数是5,标准差是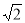 ,则
,则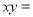 ( )
( )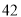 B.
B.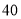 C.
C. D.
D.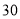

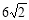 和40
和40 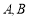 两点的坐标分别为
两点的坐标分别为 ,
, ,
,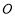 为坐标原点,动点
为坐标原点,动点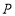 满足
满足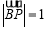 ,则
,则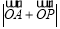 的最小值是( ).
的最小值是( ).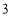 B.
B.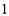 C.
C. D.
D.
 为座位号),并以输出的值作为下一个输入的值.若第一次输入的值为8,则第三次输出的值为( ).
为座位号),并以输出的值作为下一个输入的值.若第一次输入的值为8,则第三次输出的值为( ).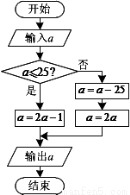
 满足
满足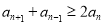 (
(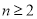 ),则称数列
),则称数列 的公差为
的公差为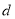 ,
,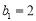 ,且数列
,且数列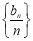 是凹数列,则
是凹数列,则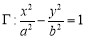 (
( )的右焦点
)的右焦点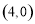 到其渐近线的距离为
到其渐近线的距离为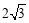 ,则双曲线
,则双曲线 的离心率为( ).
的离心率为( ).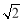 B.
B.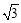 C.2 D.4
C.2 D.4 =
= ,则
,则 = .
= .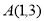 到直线
到直线 的距离为
的距离为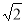 ,求直线
,求直线 的方程.
的方程.