题目内容
有下列4个命题:
①函数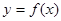 在一点的导数值为
在一点的导数值为 是函数
是函数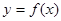 在这点取极值的充要条件;
在这点取极值的充要条件;
②若椭圆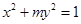 的离心率为
的离心率为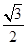 ,则它的长半轴长为1;
,则它的长半轴长为1;
③对于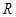 上可导的任意函数
上可导的任意函数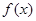 ,若满足
,若满足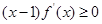 ,则必有
,则必有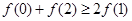
④经过点(1,1)的直线,必与椭圆 有2个不同的交点。
有2个不同的交点。
其中真命题的为 (将你认为是真命题的序号都填上)
①函数
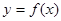 在一点的导数值为
在一点的导数值为 是函数
是函数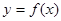 在这点取极值的充要条件;
在这点取极值的充要条件;②若椭圆
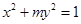 的离心率为
的离心率为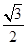 ,则它的长半轴长为1;
,则它的长半轴长为1;③对于
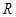 上可导的任意函数
上可导的任意函数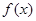 ,若满足
,若满足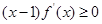 ,则必有
,则必有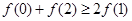
④经过点(1,1)的直线,必与椭圆
 有2个不同的交点。
有2个不同的交点。其中真命题的为 (将你认为是真命题的序号都填上)
(3)(4)
试题分析:对于①函数
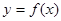 在一点的导数值为
在一点的导数值为 是函数
是函数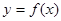 在这点取极值的充要条件;错误,应该是必要不充分条件。
在这点取极值的充要条件;错误,应该是必要不充分条件。②若椭圆
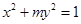 的离心率为
的离心率为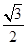 ,则它的长半轴长为1;由于焦点位置不定,应该有两个值,长半轴的长为=
,则它的长半轴长为1;由于焦点位置不定,应该有两个值,长半轴的长为= 或者1,错误。
或者1,错误。③对于
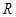 上可导的任意函数
上可导的任意函数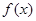 ,若满足
,若满足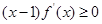 ,则必有
,则必有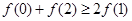 ,利用函数单调性,当x>1,地增函数,当x<1,递减函数可知不等式成立。
,利用函数单调性,当x>1,地增函数,当x<1,递减函数可知不等式成立。④经过点(1,1)的直线,必与椭圆
 有2个不同的交点,由于点在椭圆内部,可知必然有两个交点,成立,故答案为(3)(4)
有2个不同的交点,由于点在椭圆内部,可知必然有两个交点,成立,故答案为(3)(4)点评:主要是考查了命题真假的判定,以及极值概念和直线与圆锥曲线交点问题,属于中档题。

练习册系列答案
相关题目
 :方程
:方程 有两个不等的 负实根,
有两个不等的 负实根, :方程
:方程 无实根。若
无实根。若 的取值范围。
的取值范围。 那么
那么 是( )
是( )



 是两个命题
是两个命题 ,
, 是
是 的 条件。 (填“充分而不必要”、“ 必要而不充分”、“ 充分必要 ”、“ 既不充分也不必要”中的一个)
的 条件。 (填“充分而不必要”、“ 必要而不充分”、“ 充分必要 ”、“ 既不充分也不必要”中的一个)

 的充要条件是
的充要条件是

 是
是 的充分条件
的充分条件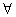 x∈R,
x∈R,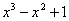 ≤0”的否定是“
≤0”的否定是“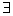
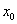 ∈R,
∈R,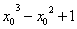 >0”;
>0”;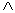 q”为假命题,则p、q均为假命题;
q”为假命题,则p、q均为假命题;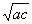 ”的既不充分也不必要条件
”的既不充分也不必要条件 是偶函数
是偶函数 的最小正周期是
的最小正周期是 ;
; 在
在 上是增函数;
上是增函数; 的图像的一条对称轴为直线
的图像的一条对称轴为直线 ,则
,则 .
. ,
, ”的否定是 .
”的否定是 .