题目内容
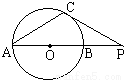
如图过点A作圆O的一条切线AB，切点为B，OA交圆O于点C．若OC=CA，BC=1，则AB=| 3 |
| 3 |
分析：连接OB，根据切线的性质，可得△OAB为直角三角形，进而结合OC=CA，BC=1，可求出圆的半径，进而求出AB
解答：
解：连接OB
则在Rt△OAB中，OB=OC=CA=R，
∴OA=2R
∴∠A=30°
∴∠AOB=60°
∴△OBC为等边三角形
故OC=OB=BC=1
∴AB=
故答案为：
解：连接OB则在Rt△OAB中，OB=OC=CA=R，
∴OA=2R
∴∠A=30°
∴∠AOB=60°
∴△OBC为等边三角形
故OC=OB=BC=1
∴AB=
| 3 |
故答案为：
| 3 |
点评：本题考查的知识点是切割线定理，做出恰当的辅助线，创造切割线定理的使用条件是解答的关键．
练习册系列答案
相关题目
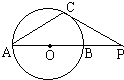C．如图⊙o的直径AB=6cm，P是AB的延长线上一点，过点P作⊙o的切线，切点为C，连接AC，若∠CPA=30°，则PC=
（2013•海淀区一模）如图，AP⊙O切于点A，交弦DB的延长线于点P，过点B作圆O的切线交AP于点C．若∠ACB=90°，BC=3，CP=4，则弦DB的长为
，过点P作圆C的切线，则两条切线夹角的正切值是________．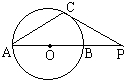
C．如图⊙o的直径AB=6cm，P是AB的延长线上一点，过点P作⊙o的切线，切点为C，连接AC，若∠CPA=30°，则PC=________．
，过点P作圆C的切线，则两条切线夹角的正切值是 ．