题目内容
已知点A、B的坐标分别是(0,-1)、(0,1),直线AM、BM相交于点M,且它们的斜率之积为- .
.(1)求点M轨迹C的方程;
(2)若过点D(0,2)的直线l与(1)中的轨迹C交于不同的两点E、F,试求△OEF面积的取值范围(O为坐标原点).
【答案】分析:(1)设出点M的坐标,写出直线AM、BM的斜率,由斜率之积为- 列式求M得轨迹方程;
列式求M得轨迹方程;
(2)设出直线l的方程,和椭圆方程联立后化为关于x的一元二次方程,利用根与系数关系写出两交点横坐标的和与积,把△OEF的面积转化为△OED与△OEF的面积的差,然后代入根与系数关系,换元后利用基本不等式求最值.
解答:解:(1)设点M的坐标为(x,y),
∵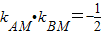 ,∴
,∴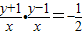 .
.
整理得,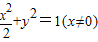 ;
;
(2)由题意知直线l的斜率存在,设l的方程为y=kx+2.
联立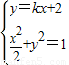 ,得(2k2+1)x2+8kx+6=0.
,得(2k2+1)x2+8kx+6=0.
由△=64k2-4×6(2k2+1)>0,解得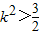 .
.
设E(x1,y1),B(x2,y2),
则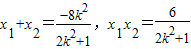 .
.
S△OEF=S△OED-S△OFD=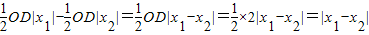
=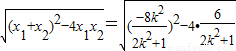 =
=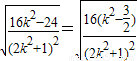 .
.
令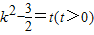 ,所以
,所以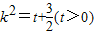 .
.
则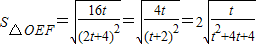 =
=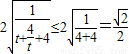 .
.
所以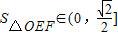 .
.
点评:本题考查了与直线有关的动点的轨迹方程,考查了直线与圆锥曲线的关系,考查了数学转化思想方法,训练了利用基本不等式求最值,利用根与系数关系解题是该类问题常用的方法,此题有一定难度.
 列式求M得轨迹方程;
列式求M得轨迹方程;(2)设出直线l的方程,和椭圆方程联立后化为关于x的一元二次方程,利用根与系数关系写出两交点横坐标的和与积,把△OEF的面积转化为△OED与△OEF的面积的差,然后代入根与系数关系,换元后利用基本不等式求最值.
解答:解:(1)设点M的坐标为(x,y),
∵
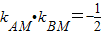 ,∴
,∴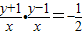 .
.整理得,
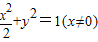 ;
;(2)由题意知直线l的斜率存在,设l的方程为y=kx+2.
联立
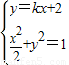 ,得(2k2+1)x2+8kx+6=0.
,得(2k2+1)x2+8kx+6=0.由△=64k2-4×6(2k2+1)>0,解得
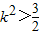 .
.设E(x1,y1),B(x2,y2),
则
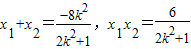 .
.S△OEF=S△OED-S△OFD=
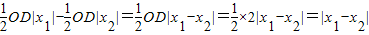
=
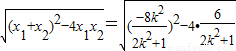 =
=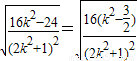 .
.令
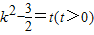 ,所以
,所以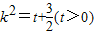 .
.则
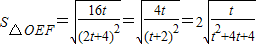 =
=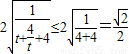 .
.所以
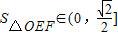 .
.点评:本题考查了与直线有关的动点的轨迹方程,考查了直线与圆锥曲线的关系,考查了数学转化思想方法,训练了利用基本不等式求最值,利用根与系数关系解题是该类问题常用的方法,此题有一定难度.

练习册系列答案
相关题目