题目内容
已知曲线y=(1)求曲线在点P(1,1)处的切线方程;
(2)求曲线过点Q(1,0)的切线方程.
解:(1)∵y′=![]() ,又P(1,1)是曲线上的点,∴P为切点,所求切线的斜率为k=f′(1)=-1.
,又P(1,1)是曲线上的点,∴P为切点,所求切线的斜率为k=f′(1)=-1.
∴曲线在P点处的切线方程为y-1=-(x-1),即y=-x+2.
(2)显然Q(1,0)不在曲线y=![]() 上,则可设过该点的切线的切点为A(a,
上,则可设过该点的切线的切点为A(a,![]() ),则该切线斜率为k1=f′(a)=
),则该切线斜率为k1=f′(a)=![]() .
.
则切线方程为y-![]() =
=![]() (x-a).(*)
(x-a).(*)
将Q(1,0)代入方程(*)得0-![]() =
=![]() (1-a),
(1-a),
得a=![]() ,故所求切线方程为y=-4x+4.
,故所求切线方程为y=-4x+4.

练习册系列答案
相关题目
已知曲线y=1-x2上一点P(
,
),则过点P的切线的倾斜角为( )
| 1 |
| 2 |
| 3 |
| 4 |
| A、30° | B、45° |
| C、135° | D、150° |
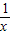 -1上两点A(2,-
-1上两点A(2,- )、B(2+△x,-
)、B(2+△x,- +△y),当△x=1时,割线AB的斜率为 .
+△y),当△x=1时,割线AB的斜率为 . ,
, ),则过点P的切线的倾斜角为( )
),则过点P的切线的倾斜角为( )