题目内容

函数f(x)=
x-2
+(x-4)0的定义域为（　　）
分析：由根式内部的代数式大于等于0，0指数幂的底数不等于0联立不等式组求解．
解答：解：要使原函数有意义，则
x-2≥0
x-4≠0
，解得：x≥2，且x≠4．
∴函数f(x)=
x-2
+(x-4)0的定义域为[2，4）∪（4，+∞）．
故选：A．
点评：本题考查了函数的定义域及其求法，关键是注意0指数幂的底数不等于0，是基础题．
练习册系列答案
相关题目
设函数f（x）=a2x2（a＞0），g（x）=blnx．
（1）若函数y=f（x）图象上的点到直线x-y-3=0距离的最小值为
2
，求a的值；
（2）关于x的不等式（x-1）2＞f（x）的解集中的整数恰有3个，求实数a的取值范围；
（3）对于函数f（x）与g（x）定义域上的任意实数x，若存在常数k，m，使得f（x）≥kx+m和g（x）≤kx+m都成立，则称直线y=kx+m为函数f（x）与g（x）的“分界线”．设a=
2
2
，b=e，试探究f（x）与g（x）是否存在“分界线”？若存在，求出“分界线”的方程；若不存在，请说明理由．
已知函数f（x）的定义域为R，则下列命题中：?
①若f（x-2）是偶函数，则函数f（x）的图象关于直线x=2对称；?②若f（x+2）=-f（x-2），则函数f（x）的图象关于原点对称；?③函数y=f（2+x）与函数y=f（2-x）的图象关于直线x=2对称；?④函数y=f（x-2）与函数y=f（2-x）的图象关于直线x=2对称．?
其中正确的命题序号是
④
④
．?

已知函数f（x）的定义域为R，则下列命题中：?
①若f（x-2）是偶函数，则函数f（x）的图象关于直线x=2对称；?②若f（x+2）=-f（x-2），则函数f（x）的图象关于原点对称；?③函数y=f（2+x）与函数y=f（2-x）的图象关于直线x=2对称；?④函数y=f（x-2）与函数y=f（2-x）的图象关于直线x=2对称．?
其中正确的命题序号是________．?
设函数f（x）=a2x2（a＞0），g（x）=blnx．
（1）若函数y=f（x）图象上的点到直线x-y-3=0距离的最小值为2
2
，求a的值；
（2）关于x的不等式（x-1）2＞f（x）的解集中的整数恰有3个，求实数a的取值范围；
（3）对于函数f（x）与g（x）定义域上的任意实数x，若存在常数k，m，使得f（x）≥kx+m和g（x）≤kx+m都成立，则称直线y=kx+m为函数f（x）与g（x）的“分界线”．设a=
2
2
，b=e，试探究f（x）与g（x）是否存在“分界线”？若存在，求出“分界线”的方程；若不存在，请说明理由．
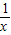下面对命题“函数f（x）=x+是奇函数”的证明不是综合法的是（ ）
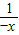A．?x∈R且x≠0有f（-x）=（-x）+=-（x+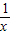）=-f（x），∴f（x）是奇函数
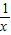B．?x∈R且x≠0有f（x）+f（-x）=x++（-x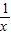）+（-）=0，∴f（x）=-f（-x），∴f（x）是奇函数
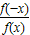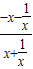C．?x∈R且x≠0，∵f（x）≠0，∴==-1，∴f（-x）=-f（x），∴f（x）是奇函数
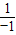D．取x=-1，f（-1）=-1+=-2，又f（1）=1+=2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网