题目内容
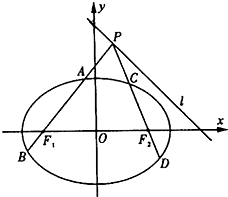
附加题:已知半椭圆
+
=1(x≥0)与半椭圆
+
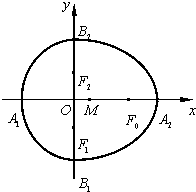
=1(x≤0)组成的曲线称为“果圆”,其中a2=b2+c2,a>b>c>0,F0、F1、F2是对应的焦点.
(1)(文)若三角形F0F1F2是边长为1的等边三角形,求“果圆”的方程.
(2)(理)当|A1A2|>|B1B2|时,求
的取值范围.
| x2 |
| a2 |
| y2 |
| b2 |
| y2 |
| b2 |
| x2 |
| c2 |
(1)(文)若三角形F0F1F2是边长为1的等边三角形,求“果圆”的方程.
(2)(理)当|A1A2|>|B1B2|时,求
| b |
| a |

(1)∵F0(c,0),F1(0,-
),F2(0,
)
∴|F0F1|=
=b=1,|F1F2|=2
=1,
于是c2=
,a2=b2+c2=
,
所求“果圆”方程为
x2+y2=1(x≥0)和y2+
x2=1(x≤0).
(2)由题意,得a+c>2b,c>2b-a,即
>2b-a.
两边平方得a2-b2>(2b-a)2,得
<
,
又b>c,b,
∴b2>c2,b2>a2-b2,
∴
>
.
∴
∈(
,
).
| b2-c2 |
| b2-c2 |
∴|F0F1|=
| (b2-c2)+c2 |
| b2-c2 |
于是c2=
| 3 |
| 4 |
| 7 |
| 4 |
所求“果圆”方程为
| 4 |
| 7 |
| 4 |
| 3 |
(2)由题意,得a+c>2b,c>2b-a,即
| a2-b2 |
两边平方得a2-b2>(2b-a)2,得
| b |
| a |
| 4 |
| 5 |
又b>c,b,
∴b2>c2,b2>a2-b2,
∴
| b2 |
| a2 |
| 1 |
| 2 |
∴
| b |
| a |
| ||
| 2 |
| 4 |
| 5 |

练习册系列答案
相关题目