Question

如图2-3-2所示，梯形ABCD中，AD∥BC，∠C=90°，且AD+BC=AB，AB为⊙O的直径，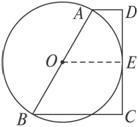

图2-3-2

求证：⊙O与CD相切.

Answer 1

思路分析：欲证⊙O与CD相切,只需证明圆心O到直线CD的距离等于⊙O的半径即可.

证明：过O点作OE⊥CD，垂足为E，∴AD∥OE∥BC.

∵O为AB的中点，∴E为CD的中点.

∴OE=(AD+BC).

又∵AD+BC=AB，

∴OE=AB=OA,即OE是⊙O的半径.

∴⊙O与CD相切.

    方法归纳 在不知道圆与直线是否有公共点的情况下,通常过圆心作直线的垂线段，然后证垂线段的长等于半径，即“作垂直，证半径”，这是证直线与圆相切的常用方法之一.